Forms of equations of parabolas:
y=ax² + bx + c
Ax² + Ey + Dx + F = 0 is the standard form equation of a vertical parabola.
Completing-the-square form: a(x+b/2a)²+(c-b²/4a).
 or, a(x-h)²+k where (h,k) is the vertex, h being a horizontal shift, k a vertical shift.
x=ay² + by + c is the equation for a horizontal parabola (which is not a function of x).
Ax² + Bxy + Cy² + Dx + Ey + F = 0, B²=4AC is the standard form equation of a general parabola, (one that can be oriented in any direction, which are discussed in conic sections)
Only vertical parabolas represent functions.

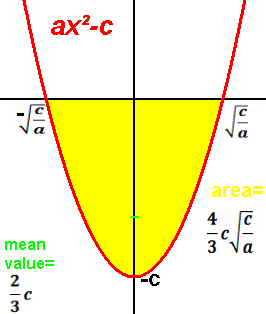
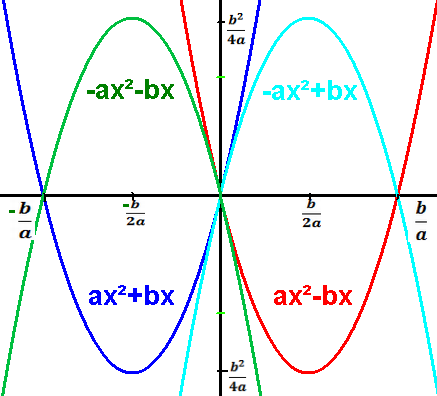
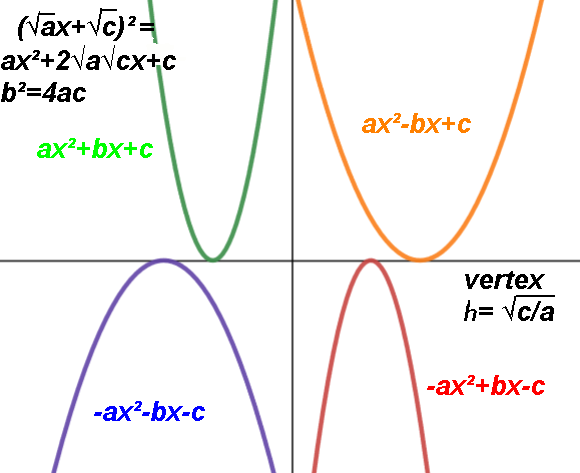
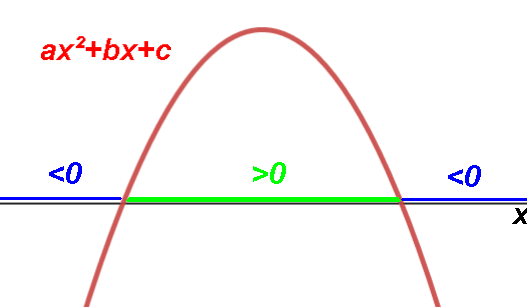
A subclass of polynomial function where the variable x is in the second power (i.e. squared) (i.e. a degree two polynomial in one variable (i.e. univariate)). a, b and c are any real numbers, a≠0 (b and/or c can be 0, i.e. they are optional).
Domain of every quadratic function is R.

Its graph in the XY Cartesian plane is a [vertical] parabola, a parabolic curve, sort of a smooth symmetric U, bowl, wok, (golden) arch, shield shape.
Parabola is one of the conic sections (slice thru a cone), along with circles, ellipses, hyperbolas.
The simplest curve?

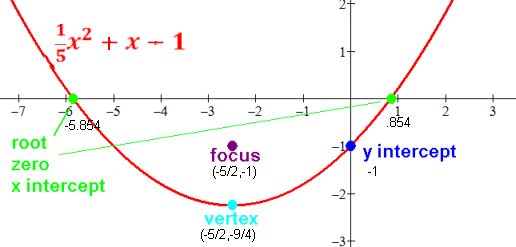
Example with all the points of interest:

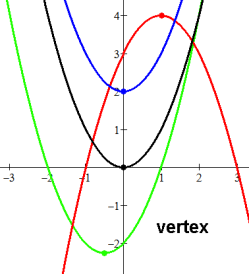
The lowest or highest point on the parabola, i.e. the smallest / minimum / nadir / bottom-of-valley or largest / maximum / zenith / top-of-hill value of the function, is the vertex:

The x-coordinate of the vertex is the average of the two x-intercepts, i.e. midway between them, which is -b/2a [even if only one or none].
The y-coordinate of the vertex is the function evaluated at this x:
    ƒ(-b/2a) = 4ac-b²/4a = c-b²/4a
So the vertex is (-b/2a,ƒ(-b/2a))

a>0: the graph is opening upward. concave up. Vertex's y is the absolute/global minimum (bottom of the valley). The two ends of the graph go up to +∞.
a<0: the graph is opening downward. concave down. Vertex's y is the absolute/global maximum (top of the hill). The two ends of the graph go down to -∞

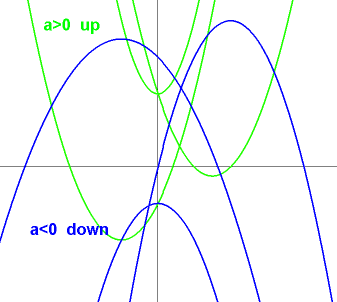
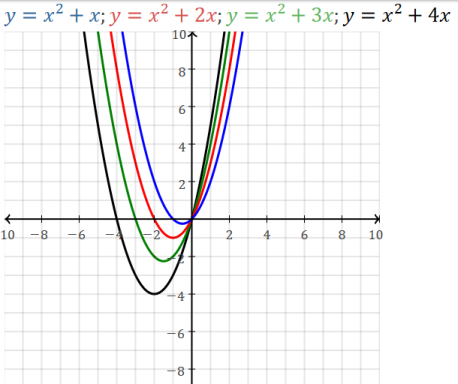
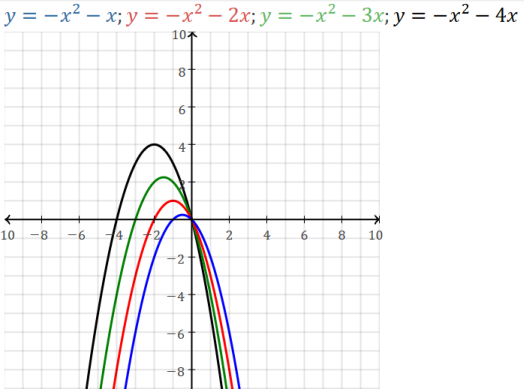
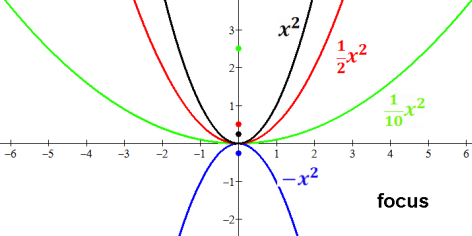
|a| is large, the sides of the curve are steep, narrow.
|a| is small, the sides of the curve are shallow, broad.

The vertex is the one turning point of the function, the point where the function changes from decreasing to increasing, or vice versa. The slope of the tangent line to the vertex is 0.

Parabola is symmetric about the vertical line [x=-b/2a] through its vertex:

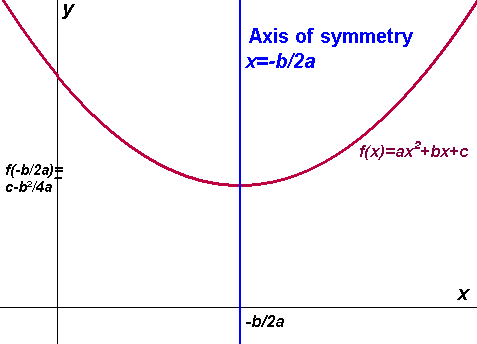
It is self-symmetric.

If there is no linear term, i.e. b=0, ƒ(x)=a(x)²+c, then the y-axis is the line of symmetry. Such functions are symmetric about the y-axis, i.e. are even functions:

Another form of every quadratic function is: ƒ(x)=a(x-h)²+k
where h is the x-coordinate of the vertex, and k the y-coordinate.
h=-b/2a, k=c-b²/4a

Range of a quadratic function:
if a>0 then range is [k,∞), or [ƒ(-b/2a),∞)
if a<0 then range is (-∞,k], or (-∞,ƒ(-b/2a]

Parabola crosses the y axis at its y-intercept: (0,c).
y-intercept is the value of setting x to be 0: a0²+b0+c = c.
Every parabola has one y-intercept.

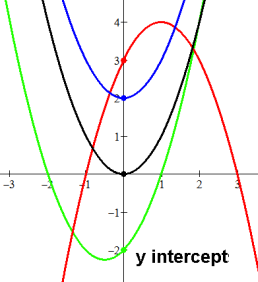
Parabola might cross the X axis at the x-intercept(s), also called the zeroes of the function or the roots of the equation.
X-intercepts' x coordinate(s) is/are the solution(s), if any, to the quadratic equation   ax² + bx + c = 0.   (i.e. y is 0)
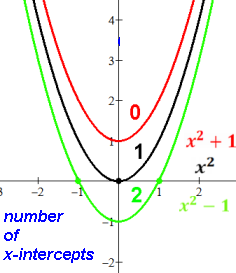
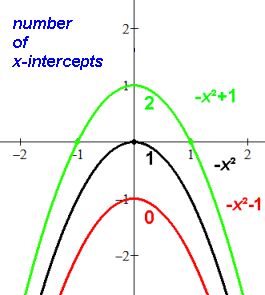
There can be 0, 1 or 2 real number solutions:
b²-4ac   is the discriminant which indicates how many (real number) zeroes/roots/x-intercepts there are:

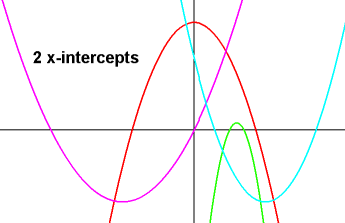
2   if the discriminant b²-4ac > 0   i.e. b>2√(ac) ∪ b<-2√(ac).
x=(-b ± √(b²-4ac)) / 2a [quadratic formula]. These two roots are unequal.

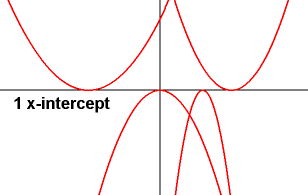
1   if the discriminant b²-4ac = 0   i.e. b=±2√(ac).
x=-b/2a.   Parabola's vertex is on the X axis. The graph touches the x-axis.
This zero has multiplicity two, i.e. it is a repeated root, a double root.
   ?These are all the perfect squares, thus the quadratic equation can be written a(x+b/2a)² = 0 or as ax²+bx+b²/(4a) = 0. and also as (√ax+b/(2√a))² = 0.

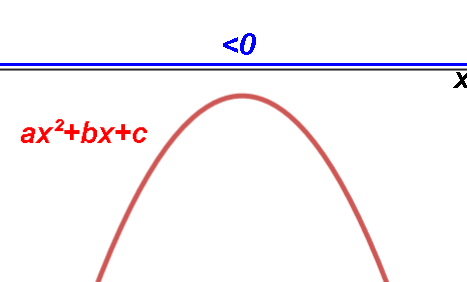
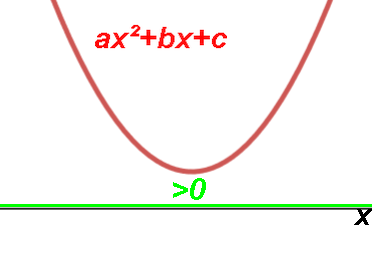
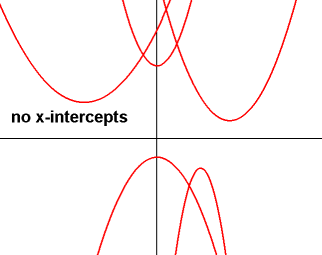
0   if the discriminant b²-4ac < 0. Parabola is completely above or below the X axis. The quadratic equation has two complex number solutions as complex conjugates   -b/2a±(√+discriminant/2a)i = (-b±√+discriminant i) / 2a.
   

The sum of the solutions/roots/zeros is -b/a. The distance between them is √(b²-4ac) /a. Their midpoint is -b/ 2a (i.e. h, the x-coordinate of the vertex).
They are a horizontal distance √(b²-4ac) /2a from the vertex.
The product of the solutions/roots/zeros is c/a.
The real zeros of ƒ(x)=ax²+bx+c are the negatives of the real zeros of g(x)=cx²-bx+a
and the reciprocals of the real zeros of h(x)=cx²+bx+a

If the parabola crosses the X axis ,i.e. the quadratic equation has 2 real roots, then both roots can be positive, both negative, or one positive and one negative:

(The 1 negative, 1 positive case might be ± the same number viz. when h=0, y-axis is the line of symmetry, b=0.)
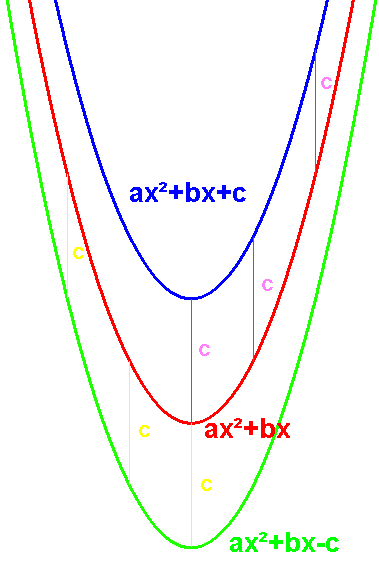
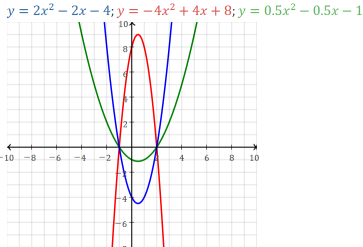
All multiples of a quadratic function have the same x-intercepts (as all multiples of a quadratic equation have the same solutions.):

Let z₁ and z₂ be the two zeroes/roots (possibly complex conjugates) of a quadratic equation, then the quadratic can be written as a pair of linear factors: a(x-z₁)(x-z₂)

Ex.

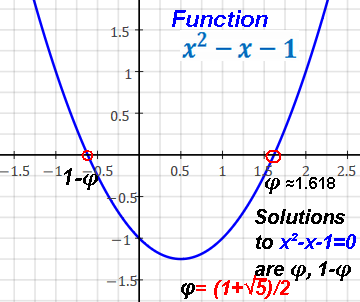
Ex. Quadratic function with the simplest complex roots:

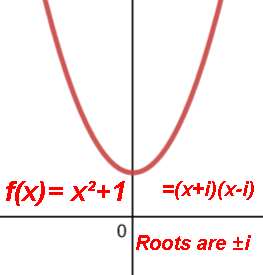
The focus of the parabola is a point on the axis of symmetry (i.e. same x as the vertex) that is 1/(4a) away: (-b/2a,(4ac-b²+1)/4a) It's in the concave bowl.

If the parabola can reflect light/radio/sound/particles, then that stuff which travels parallel to the axis of symmetry and strikes its concave side is reflected to the focus, concentrating there. Conversely, stuff that originates at the focus is reflected into a parallel beam, i.e. it can be "aimed" (gain).

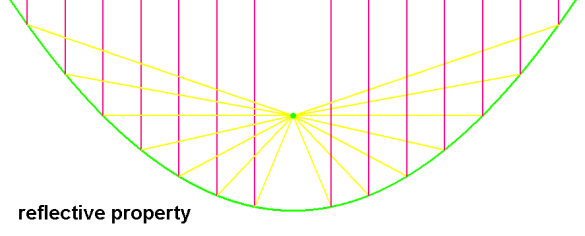
This property is used in reflecting telescopes, searchlights, flashlights, headlamps, solar cookers, satellite dishes, parabolic antennas.
A parabola rotated/spun 360° forms a 3D surface called a paraboloid.

A geometric definition of parabola as a conic section.