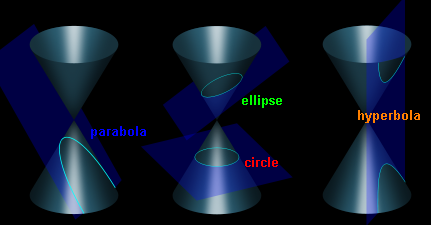
Cross-section of slices thru a double-napped (right circular) cone.


| Conic section | e | Equations | ||
|---|---|---|---|---|
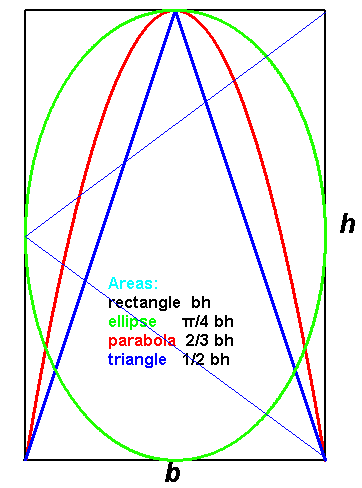
| Circles | 0 | center at origin: | Ax2+Cy2+F=0, A=C | x2+y2=r2 |
| general: | Ax2+Cy2+Dx+Ey+F=0, A=C | (x-h)2+(y-k)2=r2 | ||
| Ellipses | 0<e<1
√(1-b2/a2) | orthogonal,center at origin: | Ax2+Cy2+F=0, A≠C, AC>0 | x2/a2 + y2/b2 = 1 |
| orthogonal,center not at origin: | Ax2+Cy2+Dx+Ey+F=0, A≠C, AC>0 | (x-h)2/a2 + (y-k)2/b2 = 1 | ||
| general: | Ax2+Bxy+Cy2+Dx+Ey+F=0, B2<4AC | |||
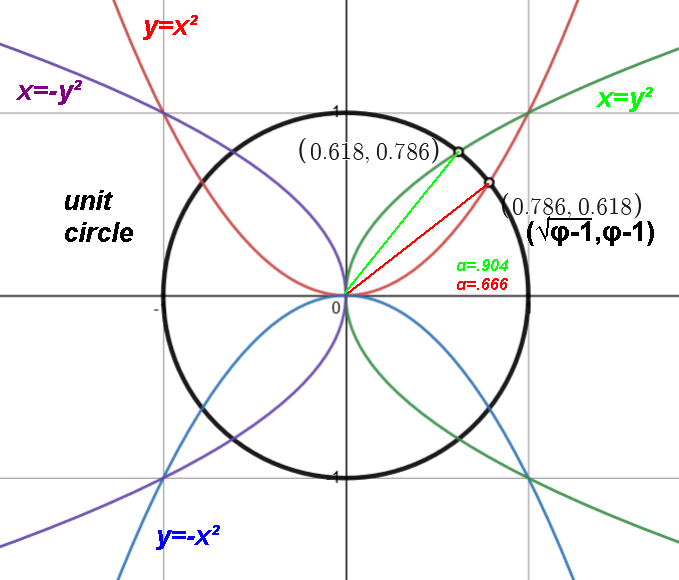
| Parabolas | 1 | vertical: | Ax2+Dx+Ey+F=0, AC=0 | y=ax2+bx+c |
| horizontal: | Cy2+Dx+Ey+F=0, AC=0 | x=ay2+by+c | ||
| general: | Ax2+Bxy+Cy2+Dx+Ey+F=0, B2=4AC | |||
| Hyperbolas | >1
√(1+b2/a2) | vertical, center at origin: | -Ax2+Cy2+F=0, AC<0 | |
| horizontal, center at origin: | Ax2-Cy2+F=0, AC<0 | |||
| general: | Ax2+Bxy+Cy2+Dx+Ey+F=0, B2>4AC | |||