Quadratic formula to solve quadratic equations
Given a quadratic equation: ax2 + bx + c = 0
a, b, c are real numbers and a≠0,
you can solve it by using the quadratic formula:

Solving means finding the solutions of the equation,
i.e. the values that substituted for x make the equation true.
There can be zero, one, or two solutions.
These solutions are also the x-intercepts of the graph of
the corresponding quadratic function.
Solutions are also called roots and zeroes.
| Equation
| a
| b
| c
| # solutions
| solutions
|
| x2 = 0
| 1
| 0
| 0
| one
| 0
|
| x2 + 1 = 0
| 1
| 0
| 1
| zero
|
|
| x2 - 1 = 0
| 1
| 0
| -1
| two
| -1, 1
|
| x2 + x = 0
| 1
| 1
| 0
| two
| 0, -1
|
| x2 - x = 0
| 1
| -1
| 0
| two
| 0, 1
|
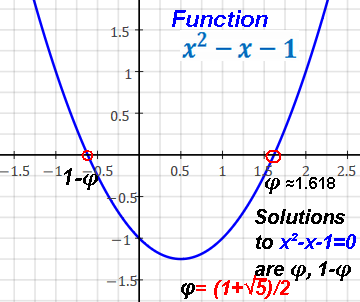
| x2 - x - 1 = 0
| 1
| -1
| -1
| two
| φ, 1-φ
|
| x2 + x - 1 = 0
| 1
| 1
| -1
| two
| -φ, φ-1
|
| x2 + x + 1 = 0
| 1
| 1
| 1
| zero
|
|
| x2 - x + 1 = 0
| 1
| -1
| 1
| zero
|
|
| x2 - 2 = 0
| 1
| 0
| -2
| two
| -√2, √2
|
| x2 - 2ex + e2 = 0
| 1
| -2e
| e2
| one
| e
|
|
|
|
|
|
|
|
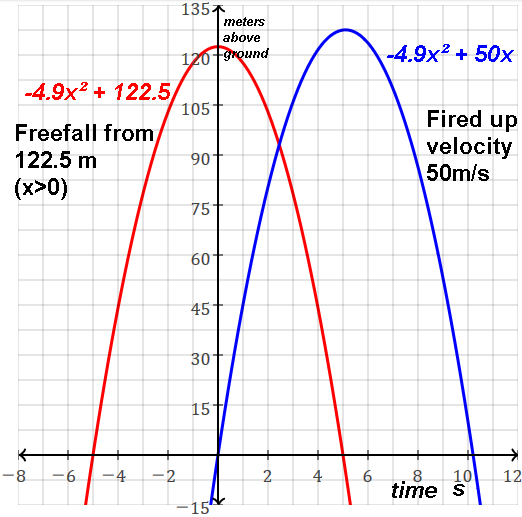
| -4.9x2 + 122.5 = 0
| -4.9
| 0
| 122.5
| two
| -5, 5
|
| -4.9x2 + 50x = 0
| -4.9
| 50
| 0
| two
| 0, 10.204
|