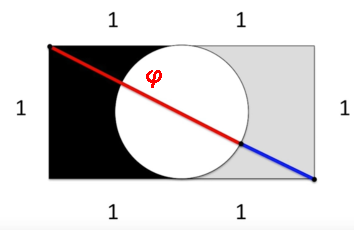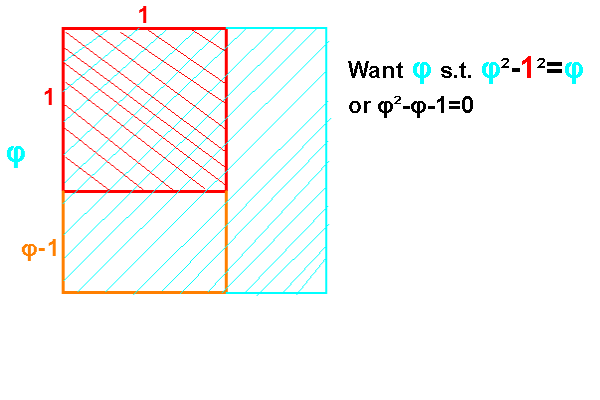
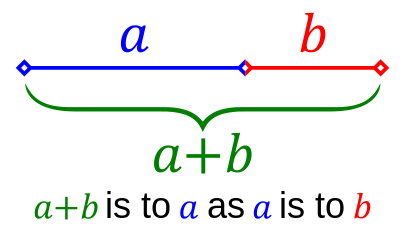
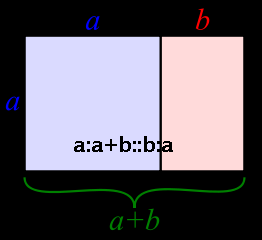
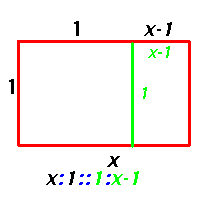
Solve x/1=1/(x-1) [similar rectangles]





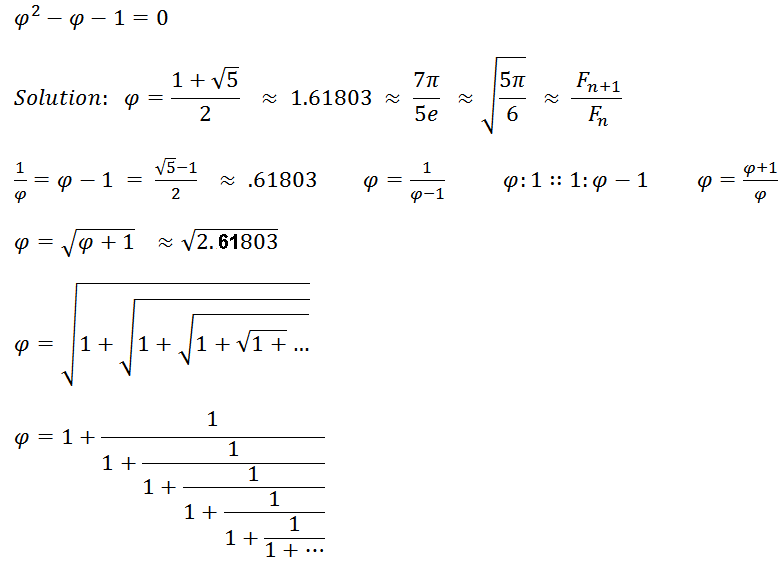
That repeated fraction is 1+1/x. Iterating 1+1/x goes to fixed point φ
Iterate it to φ
"The most irrational number." The Golden Ratio - Numberphile
"The least well-approximated irrational number".
φ is the only number whose reciprocal is one less than itself. 1/φ=φ-1
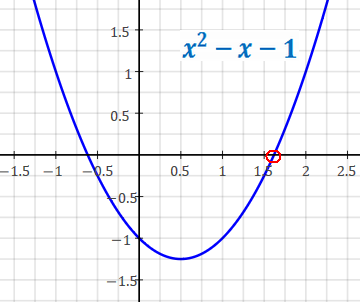
and that is equal to the square root of itself plus one: φ=√(φ+1)
Mnemonic: 1618 Defenestration of Prague
φ = 2cos(π/5) = 1+2sin(π/10) = 2sin(3π/10)

The smaller rectangle has the same ratio as the larger rectangle:
1:x-1::x-1:1-(x-1) which gives the same quadratic equation x2-x-1=0
and so on ad infinitesimal
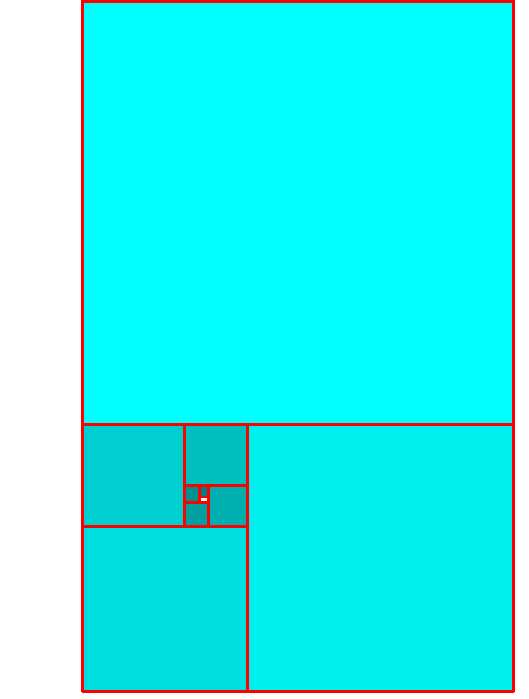
Fibonacci sequence: Fi: 1,1,2,3,5,8,13,21,34,55,89,...
Ratio of two consecutive Fibonacci numbers:
Fn / Fn-1 ≈ φ
For every Fibonacci type of sequence (start with any two numbers, next is sum of two previous...)
the ratio of two consecutive is ≈ φ.
Fn = ((1+√5)n-(1-√5)n) / 2n√5
Lucas numbers: start with 2,1, continue with Fibonacci process: 2,1, 3,4,7,11,18,29,47,... = 2,1,rounded φ2,φ3,φ4,φ5,φ6,φ7,...
∑Fi2=FnFn+1
1+1+4+9+25+64+169+441+1156+...+Fn2 =
Fn2Fn+12
The number of ways to climb steps stepping one or two at a time is a Fibonacci number.
FibonacciSteps.html
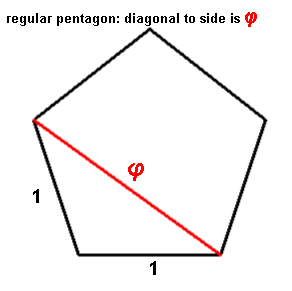
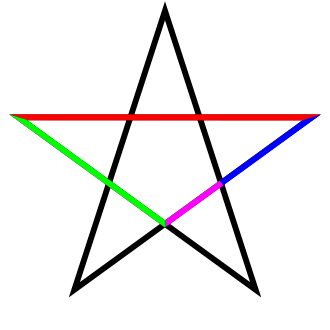
Pentagram: segments are in ratio of φ to one.