Parabola with vertex (0,k) on y-axis, with x-intercepts ±r:
y = -k/r2 x2 + k
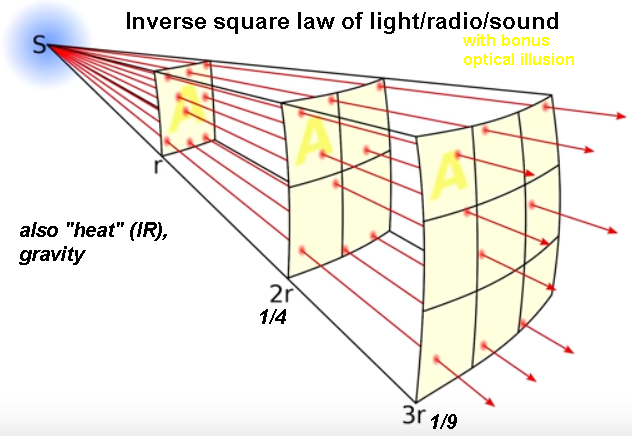
Free fall.
Distance fall pulled down by gravity, as a function of time.
d=1/2 gt2
t is seconds.
g is a constant factor, on Earth equal to 9.8 (metric) or 32 (American).
Gravity is an accelerating force: the speed (velocity) gets faster and faster.
The velocity at any time t = gt (i.e. a linear function of t).
Falling
Air resistance is ignored (i.e. not taken into consideration, as if Earth had no atmosphere).
Watch the hammer drop at 0:57
Go up, then fall down.
Height of an object shot straight up with different starting speeds, as a function of time.
d=-1/2 gt2+vot
vo is the initial velocity.
As usual, air resistance is ignored.
MPH*1.46 = ft/s
.68*ft/s = MPH
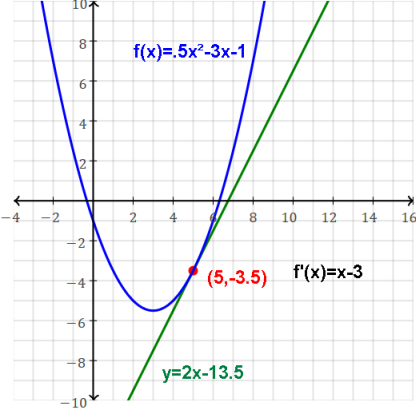
f(x)=ax2+bx+c Quadratic function.
f'(x)=2ax+b Derivative of quadratic function is linear.
Evaluated at x tells slope m of tangent line at (x,y); this slope is the
rate of change of the quadratic function at that point.
y=(2ax1+b)x+(c-ax12)
Equation of tangent line at (x1,y1)
Wikipedia Other realworld parabolas
