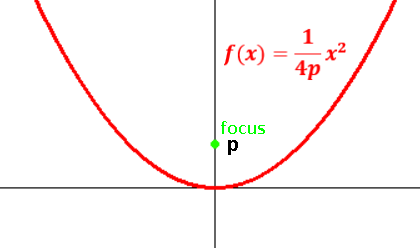
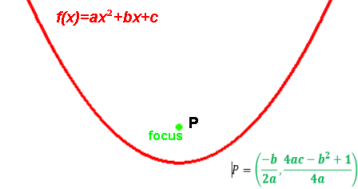

Vertical parabola with vertex (0,0), focus at (0,p) is x2=4py, or:


Vertical parabola with vertex (h,k), focus p=1/4a away is (x-h)2=4p(y-k)
Horizontal parabola with vertex (h,k), focus p away is (y-h)2=4p(x-k)
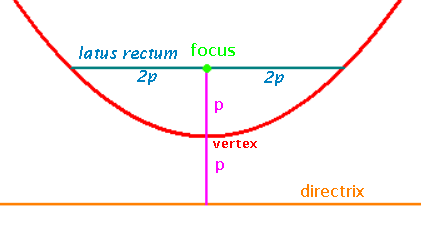
Latus rectum is line segment through the focus parallel to the directrix.
Is |4p| in length.
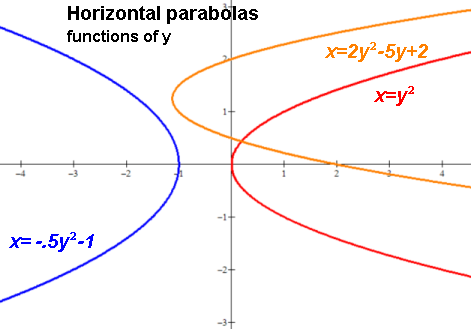
Horizontal parabola. x as a function of y.:

Oblique parabolas. Ax2+Bxy+Cy2+Dx+Ey+F=0
with B2=4AC
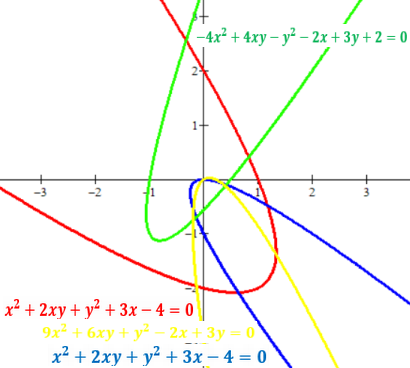
How to find the angle of rotation?
The eccentricity e of every parabola is 1.