ƒ(x) = mx + b
A subclass of polynomial function where the variable x is only in the first power
(i.e. a degree-one polynomial in one variable (i.e. univariate)).
m and b are any real numbers.
In polynomial-ish form: ƒ(x) = a1x1 + a0
All other functions are non-linear.
And/or equivalently, y = mx + b
a linear equation of two variables.
m is the slope.
b is the y-intercept.
Its graph in the xy Cartesian plane is a (straight) line.
This is why linear functions are called line-ar.
(A graph shows all the points (i.e. pairs of x and y values) that make the equation true.
And shows, for each value of x, its corresponding ƒ(x) (i.e. y) function value.)
Linear functions are the simplest functions; but very useful.
The domain of every linear function is R. The range is R too, except
for the special case of constant (horizontal) functions whose range is just one number.
Slope is the steepness/shallowness, grade, gradient, tilt, pitch, slant, incline/decline of the line.
The slope is the same at all points of the line.
Slope is how much the function is increasing or decreasing,
i.e. its rate of change,
which is how much the real-world process/activity is changing.
A linear function's rate of change is unchanging, i.e. it is the same, it is a steady rate.
Linear means wherever the x is (e.g. near -∞ or +∞ or 0)
the change of y is the same for the same change of x.
Linear function as all multiples of m.
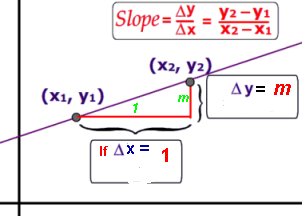
Between any two points:
--the rise over the run;
--the change in the vertical divided by the change in the horizontal;
--the change in y per one unit change in x, i.e. the rate of change of the y,
the unit rate of y's per x.
--the change in y as a percentage of x: %=m*100% (e.g. y=2x y=200%x; y=1/2x y=50%x)
Ex. a slope of 2 means for a one unit increase of X the Y increases by 2.
Ex. a slope of -2 means for a one unit increase of X the Y decreases by 2.
m = Δy / Δx
= (y2-y1)/(x2-x1) for any two points on the line.

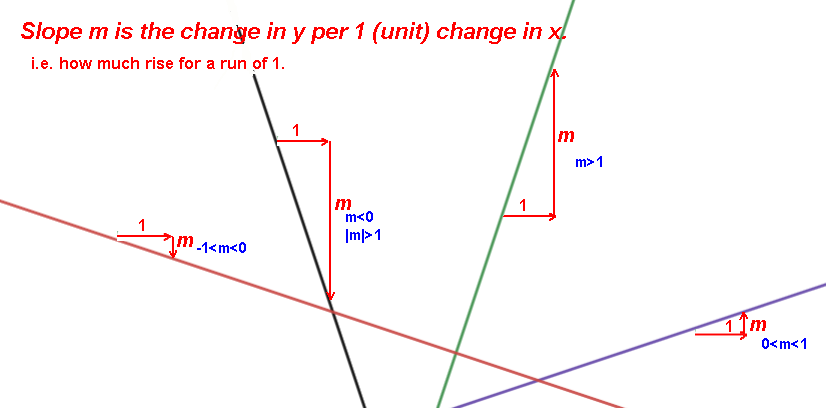
Slope Explorer demos slope.
If α is an angle in radians: m=tan(α) and m=tan(angle°*(π/180))
α=arctan(m) and angle°=arctan(m)*(180/π)
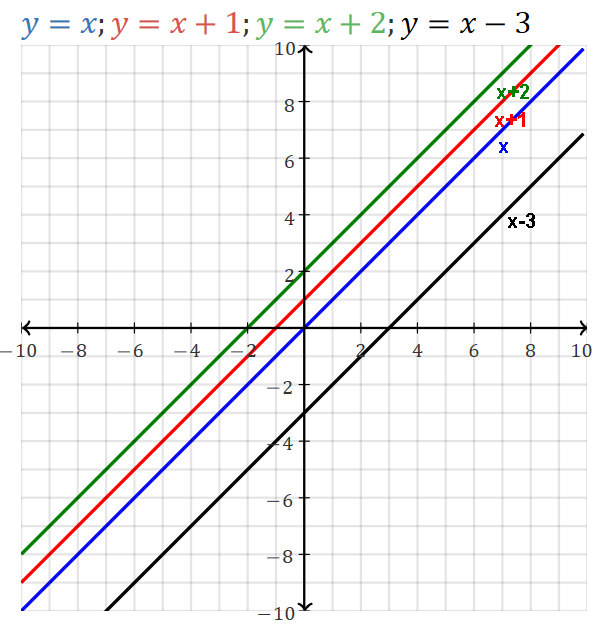
Line crosses the y axis at the y-intercept: (0,b).
If b is 0, graph crosses origin (0,0).
A nonzero b is an offset from the origin, often representing an initial value.
Line crosses the x axis at the x-intercept, also called the zero of the function: (-b/m,0).
X-intercept's x coordinate is the solution to the linear equation mx+b=0.

Every linear function's line crosses both axes.
(Except the special case of horizontal lines, see below).
One end goes up to +∞, the other goes down to -∞.
There are no extrema, turning points, inflection points.
A line through the origin has x-intercept and y-intercept at the same point, i.e. (0,0).
A line through the origin is symmetric about the origin, i.e. an odd function.
I.e. ƒ(-x)= -ƒ(x) [m(-x)=-mx] and ƒ(x)= -ƒ(-x) [mx=-m(-x)].
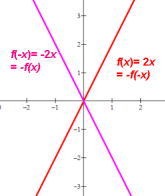
A line not through the origin is neither odd nor even.
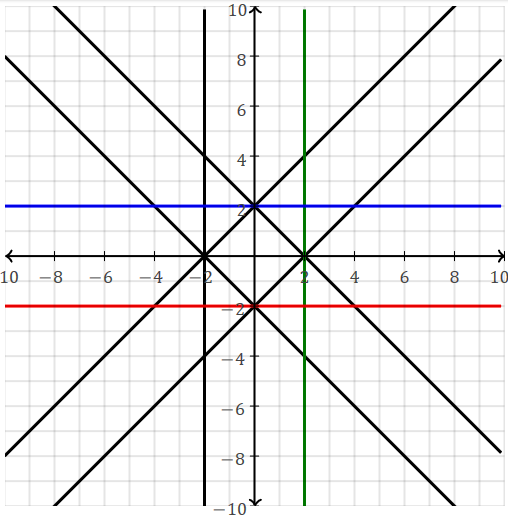
All multiples of a linear function have the same x-intercept
(as all multiples of a linear equation have the same solution):
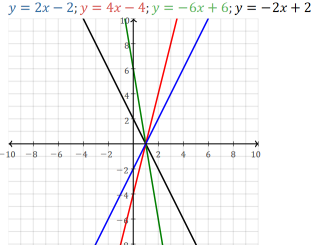
Varying the (positive) slope m, holding b at 0 (i.e. y-intercept is (0,0)).
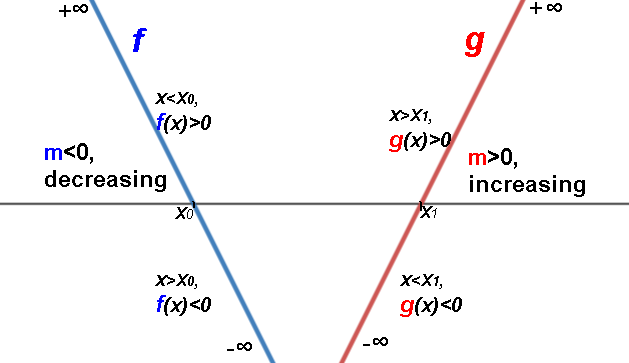
Positive slope m means function is
increasing
(rising when going from left to right on graph).
As x increases, y increases.
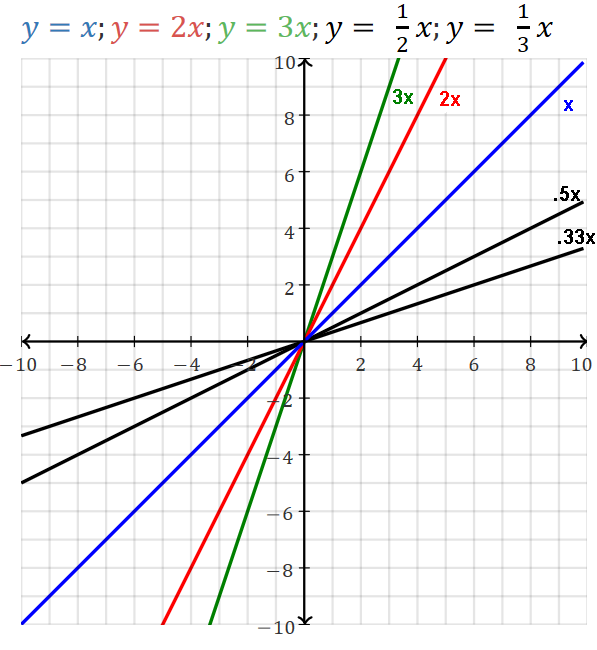
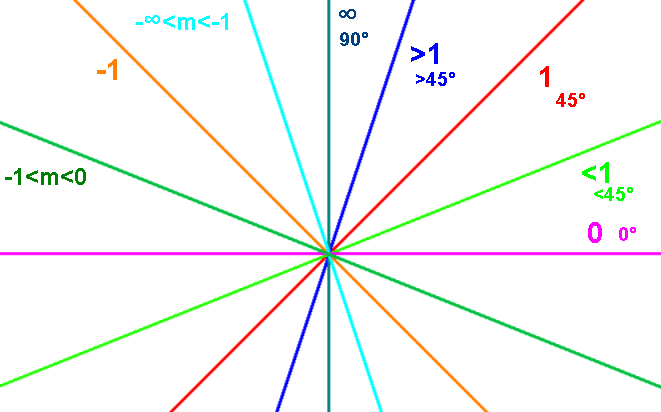
The larger the slope m, the steeper the line, the faster it rises/grows.
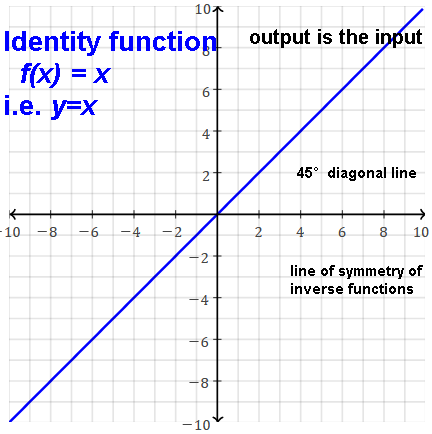
If m=1, line is the main diagonal, 45°. (this y=x is the identity function ƒ(x)=x.)
If m>1, line is >45°. If m<1, line is <45°
Varying the (negative) slope m, holding b at 0 (i.e. y-intercept is (0,0) )
Negative slope m means function is
decreasing
(falling when going from left to right on graph).
As x increases, y decreases.
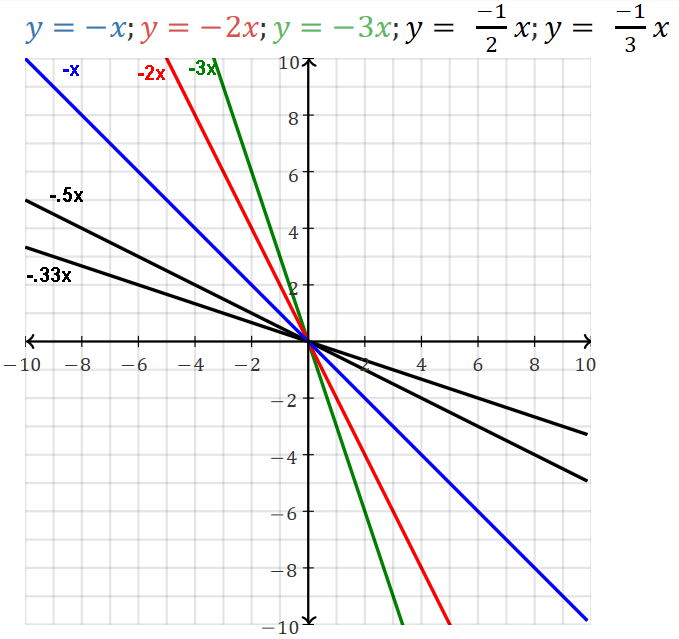
The larger the slope |m|, the steeper the line, the faster it falls.
If m=-1, line is the other diagonal, y=-x.
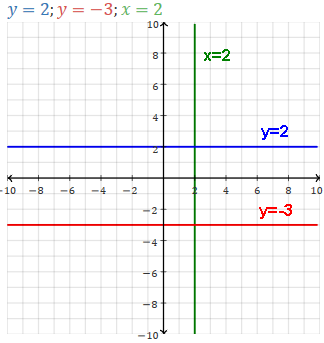
Special case: any
horizontal (flat) line has function ƒ(x)=b or y=b, where b is y-intercept.
There is no x term, so some people don't consider this a linear function.
Or it is a degree 0 polynomial function.
Slope m is 0: y=0x+b, which is y=b. The function is neither increasing nor decreasing.
There is no change in the y. For every x, the function outputs b.
It's a
constant function, the simplest kind of function, always the same, never changing.
Whatever the x input is, the output is the same.
Special special case: ƒ(x)=0 or y=0 Horizontal line is the x-axis.
Is the no-degree polynomial function.
Extra Special case: any vertical line is not even a function.
The graph does not pass the vertical line test.
Its equation is x=c.
Slope is undefined (there is no change in the x,
so the slope equation would be m=(y2-y1)/0, which would be infinite).
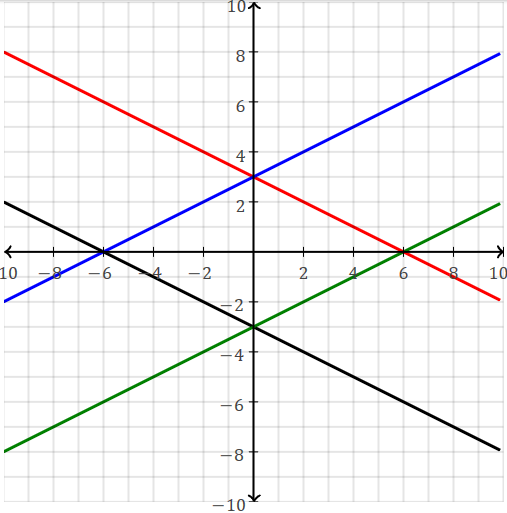
Parallel lines (i.e. don't intersect; no points in common)
have same slope m. Linear functions with same slope m are parallel lines.
They differ in their y-intercept b.
The distance of the gap between two parallel lines is:
cos(arctan(m))*|b
1-b
2|, and also
|b
1-b
2| / √(m
2+1)
Between two parallel lines are an infinite number of parallel lines.
Perpendicular lines (i.e. lines that meet at right angles) have slopes that
are the negative reciprocal of each other.
i.e. product of slopes of two perpendicular lines is -1.
If the slope of a line is m, then all lines perpendicular to it have slopes -1/m.
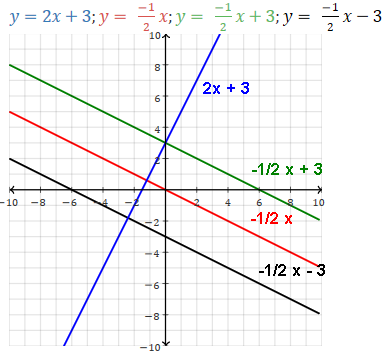
Every horizontal line is perpendicular to every vertical line, and vice versa.
Various lines:
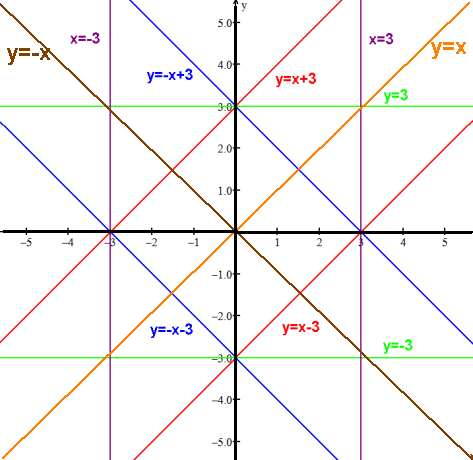
The sum, difference, and composition of two linear functions is a linear function.
Multiplying or dividing two linear functions takes you non-linear into quadratic
and rational functions, respectively.
Identity function: f(x) = x
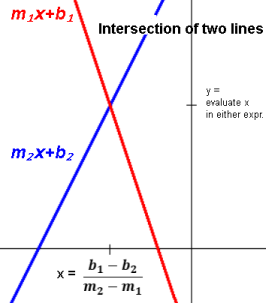
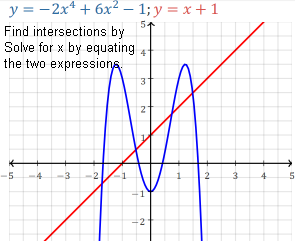
Two non-parallel lines m1x+b1 and m2x+b2 intersect where
the two expressions are equal:
xi=(b2-b1)/(m1-m2)
Secant line:
On the curve of a function ƒ
the slope of the secant line connecting any two points (a,ƒ(a)) and (b,ƒ(b))
is the average rate of change over the interval [a,b]. (On a curve, the rate of change
changes, or differs, at every point.)

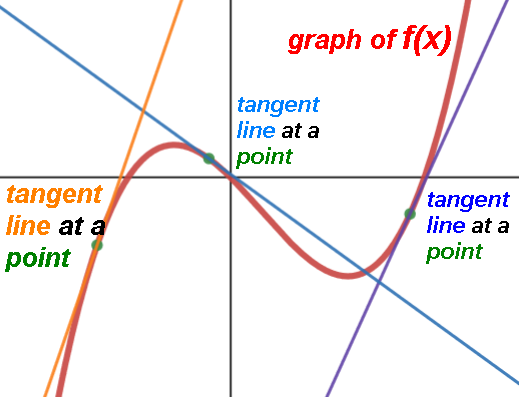
Tangent line to a curve at a point;
the one line just touching the curve at that point.
Every point on a curve has one tangent line;
each point's tangent line is different than the
tangent lines of all other points on the curve;
the tangent line is on the convex side of the curve.
Slope of the tangent line at the point is
the instantaneous change of that function
at that point, i.e. how much it is changing
at that point, its rate of change.
(Some points' different tangent lines might have the same slope.)
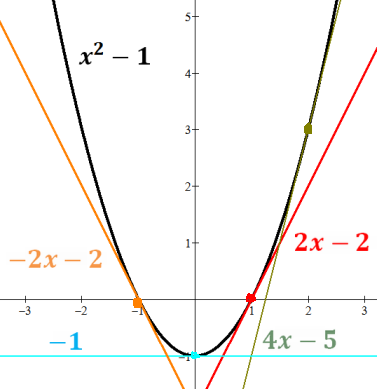
Calculus's differentiation of the function ƒ
is the function ƒ' (i.e. the derivative of ƒ)
whose evaluation for each x yields the slope of the
tangent line at the (x,y) point on the curve of ƒ.
ƒ(x) = y points on the curve of ƒ. Graph above: f(x)=x2-1
ƒ'(x) = m slope of the line tangent to curve at (x,ƒ(x)). Graph above: ƒ'(x)=2x
tangent tangible touchable
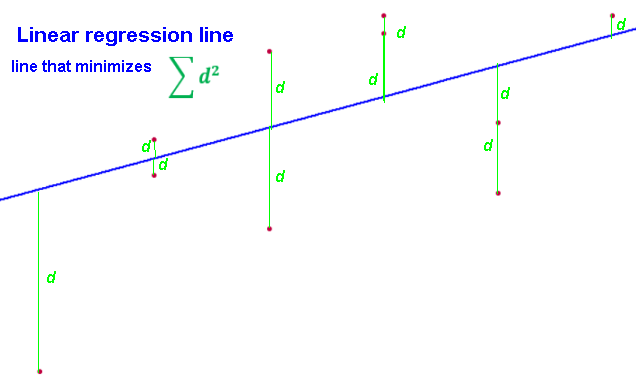
Linear regression line through a bunch of points (data):
is the "best" line for approximating the linear relationship between the X and Y variables.
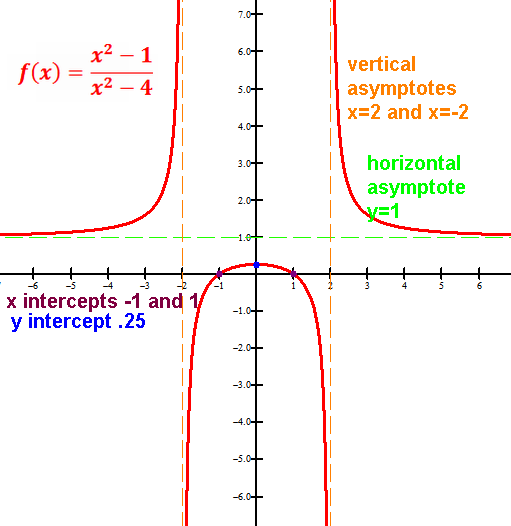
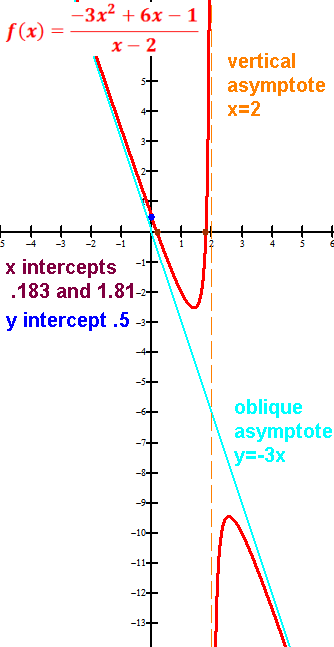
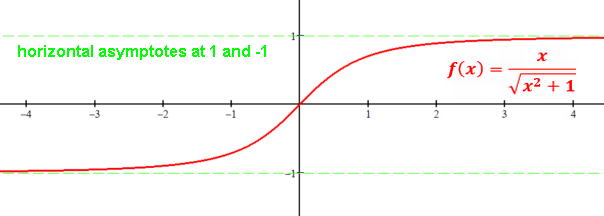
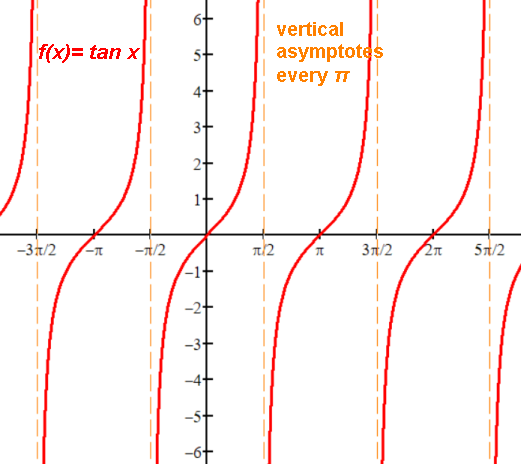
Asymptote: a line that a curve approaches but never reaches.
Vertical where x is not in domain of the function
(typically that would make the denominator 0).
horizontal as x approaches +∞ and/or -∞
slant/oblique
Worksheets. Identify all the functions and equations: