A way to combine two functions by putting them in series, sequence, pipeline, workflow, assembly line, i.e. the output of one function is the input to another.
f∘g=f(g(x))
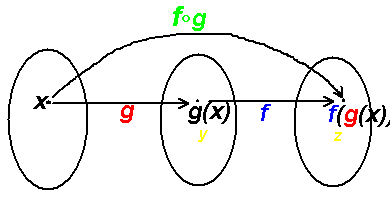
f(g(x)): Input x to g, the output g(x) is the input to f.
Note that g is done first, then its output is the input to f.
And/or form the composed function (f∘g)(x),
a new function that is the composition of f and g,
by setting each x of f's expression to
g's expression and then simplify [see below].
This new composed function f∘g will have the same effect
as doing g and f in sequence.
Composition as an operation of functions: f∘g,
cf. function arithmetic f+g, f-g, fg, f/g
g∘f=g(f(x))
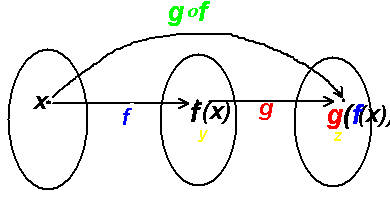
g(f(x)): Input x to f, the output f(x) is the input to g.
And/or form the composed function (g∘f)(x) by setting each x of g's expression to
f's expression and then simplify.
Functions in series: the output of one function is the input to the next function.
The composed function g∘f is composed of f and g in series:
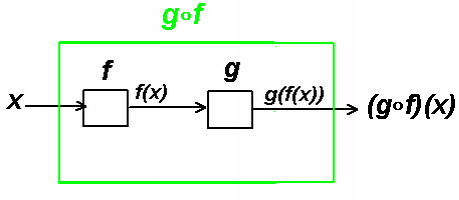
Can be useful to combine two processes (f and g) into one process
by directly connecting the input x to the output, and so by eliminate the "middle man".
f(x)=x-1 g(x)=3x f(g(0))=f(0)=-1 g(f(0))=g(-1)=-3 f(g(1))=f(3)=2 g(f(1))=g(0)=0 f(g(-2))=f(-6)=-7 g(f(-2))=g(-3)=-9 (f∘g)(x)=f(g(x))=f(3x)=3x-1 (g∘f)(x)=g(f(x))=g(x-1)=3x-3 (f∘g)(0)= -1 (g∘f)(0)= -3 (f∘g)(1)= 2 (g∘f)(1)= 0 (f∘g)(-2)= -7 (g∘f)(-2)= -9
Example: f(x)=4x+5 g(x)=√x+1
f∘g = f(g(x))=
4(g(x))+5 =
4(√x+1)+5 =4√x+9
g∘f = g(f(x))=
√(f(x))+1 = √(4x+5)+1
NB. f∘g ≠ g∘f
Example: f(x)=x2-2x g(x)=3x+1
(f∘g)(x) = f(g(x))=
(g(x))2-2(g(x)) =
(3x+1)2-2(3x+1)=9x2-1
(g∘f)(x) = g(f(x))=3(x2-2x)+1=3x2-6x+1
Composition is not commutative, so in general, f∘g does not equal g∘f. If it does, it is the identity function I(x)=x and the functions are inverses of each other.
Not limited to two functions. Composition is associative: f∘(g∘h) equals (f∘g)∘h
If the same function, e.g. f∘f=f(f(x)), the output of f fed back to be the next input to itself. AKA Iteration.
Domain of the composition f∘g is the x's in the domain of g
whose g(x)'s are in the domain of f.
Domain of the composition g∘f is the x's in the domain of f
whose f(x)'s are in the domain of g.
NB. the domain of the composition is not simply the domain of that function form,
but must include the "history" of the composed functions' domains.
Examples:
| f | g | f∘g f(g(x)) | g∘f g(f(x)) |
|---|---|---|---|
| 3x-2 | -2x+5 | -6x-13 | -6x+9 |
| 3x | x2 | 3x2 | 9x2 |
| 4x+9 | √x | 4√x+9 | √(4x+9) |
| x3 | x2+1 | (x2+1)3 | x5+1 |
| sin3x | 4x | sin34x | 4sin3x |
| ln2x | x2+3x+2 | ln(2x2+6x+4) | (ln2x)2+3(ln2x)+2 |
linear ∘ linear = linears with same slope: m1m2, i.e. parallel lines
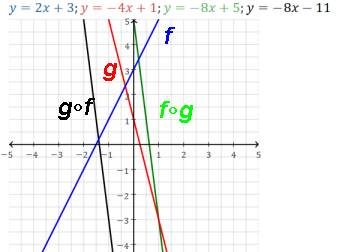
linear ∘ quadratic = quadratic
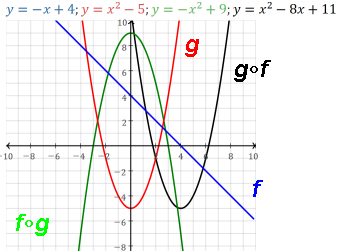
quadratic ∘ quadratic = quartic
polynomial ∘ polynomial = polynomial
The composition of two odd functions is odd.
The composition of an odd function with an even function is even.
Book's example:
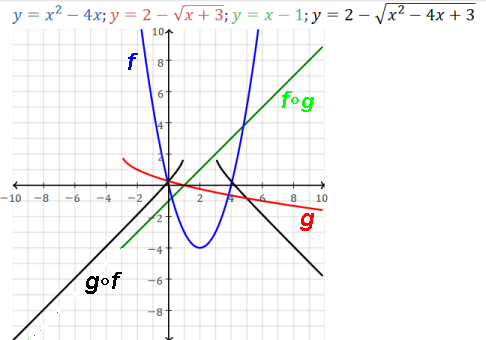
Domain of f is R. Domain of g is [-3,∞) Domain of f∘g is [-3,∞) Domain of g∘f is (-∞,1]∪[3,∞)
Composition as a [binary] operation of functions,
cf. function addition, subtraction, multiplication, division (mind the denominator).
(f+g)(x) = f(x)+g(x)
Add the functions' expressions to form a sum function f+g and then evaluate input x
OR input x to each function and then add the outputs.
Example: f(x)=2x2+x-√(3x2) g(x)=-4x+2
f(2)=6.535898 g(2)=-6 f(2)+g(2)=0.535989
(f+g)(x)=2x2-3x-√(3x2)+2 (f+g)(2)=0.535989
Domain of the sum (f+g)(x) function (or
difference function (f-g)(x), product function (fg)(x), quotient function (f/g)(x))
is the intersection of the domains of f and g.
[quotient function has the additional restriction of excluding any value that makes g(x)=0]
In calculus, the Chain Rule is used to differentiate a composed function:
f(g(x))' = f'(g(x))g'(x)