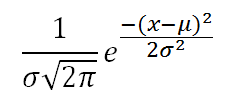Measures the spread of the data around the mean, i.e. its variation.
An average of how much the data deviates from or around the mean.
A measure of how much we can expect a value to differ from the center.
A measure of the uncertainty there is for any data value.
The more spread out, the more dispersed, the more scattered the data, the larger its standard deviation.
The larger the standard deviation is, the more spread out and dispersed the data.
The more clustered and huddled the data, the smaller its standard deviation.
Definition and formula for the standard deviation:
s is the sample standard deviation.
The xi are the data values, x̄ is the sample mean,
n is the number of data values.
Take the difference between each data value and the mean (the datum's deviation),
square that and
sum those squared differences (this is the "sum of squares", SS),
divide by n-1 for a kind of average, and then take the square root of that
(to "un-do" the squarings and get back the original un-squared
units of the data [m, kg, s, B, W, etc.]).
σ is the population standard deviation.
Uses the population mean μ and divides by N.
s is always larger than σ but not by much except for small n and N.
NB. Sometimes, someplaces s is denoted by σn-1 and σ by σn
Webpage to calculate statistics, including standard deviations.
Alternate "computational" formula for s. Note it doesn't need the mean.
Exs.:
This data: 1 2 3 4 5 6 7 8 9 10 has a mean of 5.5 and a standard deviation of 2.87.
This data: 0 2 3 4 5 6 7 8 9 11
same mean of 5.5 but a wider spread, and so its standard deviation is larger, at 3.20.
This data: 1 2 3 5 5 5 7 8 9 10 mean of 5.5 but is more "clustered",
and its standard deviation is 2.83.
This data: 2 2 3 5 5 5 7 8 9 9 is more clustered yet, and so its standard deviation is 2.53.
The standard deviation is not the range.
This data: 2 4 4 5 5 5 5 6 6 14 has the largest range of these examples but not the largest
standard deviation (its is 3.00).
Nor is it related directly to the number of different data values.
This data: 1 1 1 5 5 5 5 10 10 10 has the fewest number of different data values
but a large standard deviation of 3.49.
If the data is all the same, the standard deviation is zero.
There is no variation among the data, it is all [clustered] at the mean.
Ex.: This data: 10 10 10 10 10 10 10 10 10 10 has σ = 0
If the data is perfectly bi-modal, the population standard deviation is one half
the range, which is the distance from the mean to either datum,
which is the mean [absolute] deviation (MAD, the average distance of a datum
from the mean). Otherwise, σ > MAD
Ex.: This data: 10 10 10 10 10 20 20 20 20 20 has σ = 5 = MAD
Exs.
Ex.: The red and blue dots have the same average (at the center of the image)
but different standard deviations (red data's SD is larger than the blue data's SD):
Without knowledge of the standard deviation, the mean is incomplete.
Standard deviation complements the mean; shouldn't have one without the other.
These data sets have the same mean and the same range:
1 1 1 1 1 9 9 9 9 9 9
1 5 5 5 5 5 5 5 5 9 9
but you wouldn't want to leave it at that. SD will help characterize their differences.
SD of the first is 3.98, the second 2.06.
The standard deviation is the square root of the variance, VAR.
Population: σ2. Sample: s2.
Different equivalent formulae for it:
(sample variance has n-1 in place of N).
There isn't a geometric or intuitive idea of what the standard deviation is,
except that it is ≥ the average distance of the data from the mean, i.e. MAD.
MAD
1 2 3 4 5 6 7 8 9 10 has SD=2.87
Adding the same constant c to each data value does not change the SD.
Add c=100 to each of those numbers gives 101 102 103 104 105 106 107 108 109 110
whose SD is 2.87
Multiplying all the data values by a constant k multiplies the SD by the same number.
Multiplying each of those numbers by k=10 gives 10 20 30 40 50 60 70 80 90 100
whose SD is 28.7
Duplicating etc. every datum has no effect on the SD.
The mean is a balance point, half the data is less than it, half greater.
The standard deviation is a "natural" measure of dispersion when the
"center"/"middle" of the data is the mean.
This is because the standard deviation from the mean is smaller than
from any other point, i.e.
it is minimized when calculated, as it is, from the mean μ or x̄.
It would be larger if any other point were used in the formula.
Coefficient of variation:
sample CV = s / x̄ or population CV = σ / μ
Expressed as a percentage. Basically, is the percent that the SD is of the mean.
How much the data varies compared to the mean.
A measure of the spread of the data relative to the average of the data.
Useful for comparing data sets whose means are very different or use different measuring units.
| At least this much of the data | are within this of the mean, μ |
| 50% =1/2 | ±√2σ |
| 75% =3/4 | ±2σ |
| 88.88% =8/9 | ±3σ |
| 93.75% =15/16 | ±4σ |
| 96% =24/25 | ±5σ |
A normal/Gaussian probability distribution function is characterized/defined by its mean μ and σ.
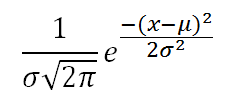
Here are the graphs of three normal distribution functions with the same mean of 10 but
different standard deviations of 1, 2, and 3:
u=10, blue s=1, red s=2, green s=3
The area under the curve of each function is the same, i.e. 1.
The smaller the σ, the narrower and taller the curve, the more clustered around the mean.
The larger the σ, the wider and shorter the curve, the more dispersed around the mean.
Empirical Rule of a Normal Distribution:
~68% of data within 1 σ of mean,
~95% of data within 2 σ,
~99.7% of data within 3 σ
One σ from the mean is an inflection point,
where the concavity changes sign,
where the second derivative is zero,
where the slope (rate of change) is at a maximum or a negative minimum.
| Probability Distribution function | Standard deviation | MAD |
|---|---|---|
| Uniform | range/√12 | range/4 |
| Normal | σ | σ√(2/π) |
| Binomial | √(np(1-p)) | |
| Poisson | √λ | |
| Χ2 | √(2k) | |
| Exponential | 1/λ | |
| t | √(df/(df-2)), df>2 | |
| Lognormal | eμ+σ2/2√(eσ2-1) | |
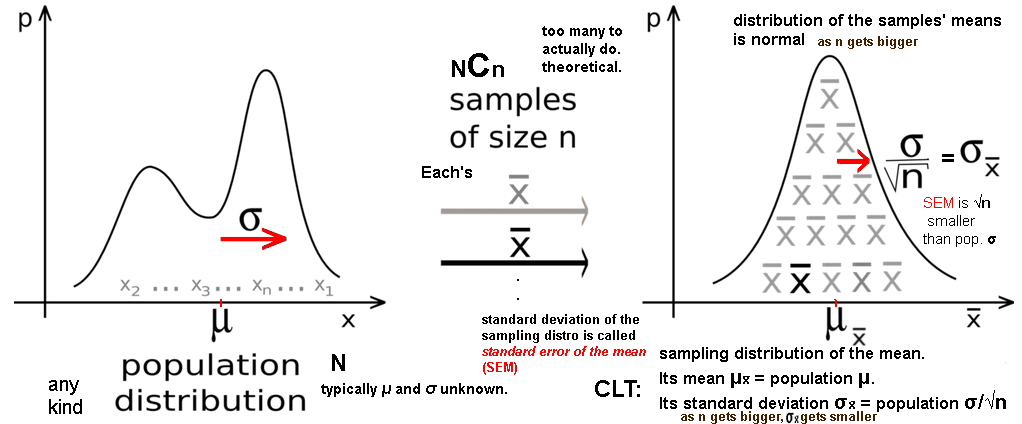
Central Limit Theorem:
