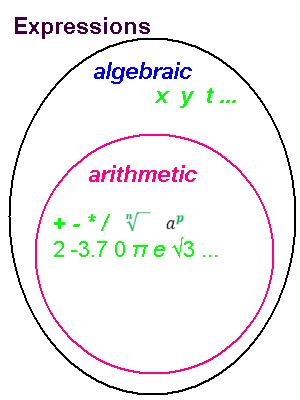
Arithmetic expression: numbers and operators. PEMDAS order. No variables.
Exs.    5+6-2(3-√25)2     you evaluate / simplify / reduce / calculate / find-the-value / figure-out-what-it-equals / "boil down"    to 3
7(2)2 - 3(2) + 4    = 26
7(3)2 - 3(3) + 4    = 58
7(4)2 - 3(4) + 4    = 104
Ex.   3π√(32+22)    = 3π√13    ≈ 33.98152

Semi-exception: irrational term might preclude reduction to single number:
Ex.   7(√2)2 - 3√2 + 4    = 18 - 3√2    can be approximated to ≈ 13.757359

Numbers are like words, expressions are like phrases.

An arithmetic expression is a (restricted) algebraic expression:

       

Exs:
   6x
   4πr2
   2x + 5
   7x2 - 3x + 4
   3x2yz3 + y - 4x
   -1.23√(2x+5) + 4
   (7x2+3x+4) / (2x+5)
   3·3.212x+5 + 4
   3·log(2x+5) + 4
   3·sin(2x+5) + 4
   6

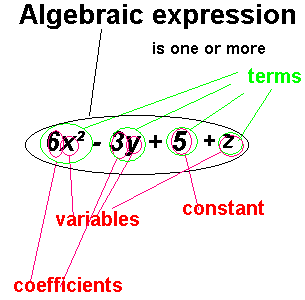
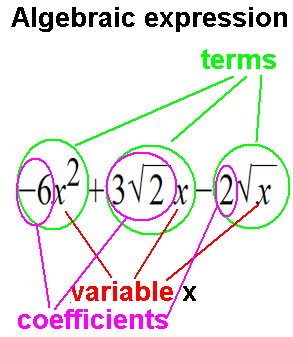
An algebraic expression is a pattern / mold / recipe / template for some/many/all possible arithmetic expressions that fit the pattern.
It's the general form of a bunch of arithmetic expressions that all are of that form.
For any/every number, do certain operations in a certain (PEMDAS) sequence.
"Seven times the square of a number less three times the number and then add four." → 7x2 - 3x + 4

Variable is a placeholder. Letters are used to indicate variables. Could have been boxy symbols:
7▢2-3▢+4    instead of   7x2-3x+4   to convey the idea that the variable can be or take on any number (fill in the box).
(Different variables need different boxes: 3▢-5△+4   instead of   3x-5y+4)
Algebraic expression: a fill-in-the-blank recipe for arithmetic. Plug in any number for the variable (x), and you get a specific result — but the expression itself works for all possible numbers.

In an application the variables could represent some quantity of stuff such as time, money, energy, mass, temperature, length, area, volume, number of people or products, etc.
Typically, a more mnemonic letter is used, e.g. t for time.
Ex.   5/9(F-32)    F is temperature in fahrenheit
Ex.   ½bh    b is base, h is height of a triangle
Ex.   P(1+r)t    P is the principle (lump of money), r is the interest rate, t is years.
Ex.   -4.9t2+vt    t is time in seconds, v is velocity in m/s

NB. an expression does not have a graph, pace Desmos: (you can enter an expression of one variable [only x] and it is turned into a function, as a convenience for you)

What can be done with an algebraic expression:

  1. Evaluate it by substituting a value (number) for each different variable and then calculating the resulting arithmetic expression.
    Instantiate it.
    Ex.    Evaluate 7x2-3x+4
    when x is 2 → 7(2)2-3(2)+4 = 26
    when x is 3 → 7(3)2-3(3)+4 = 58
    when x is 0 → 7(0)2-3(0)+4 = 4
         0 is the "best" number to evaluate with because it makes every term containing the variable zero i.e. "disappear".
         And 0 often means starting value, nothing, no time, no money, etc.
    when x is 1 → 7(1)2-3(1)+4 = 8
    when x is 1.234 → 7(1.234)2-3(1.234)+4 = 10.957292
    Note: the evaluation results in a single number; the same each time. The expression "determines" the result.

  2. Determine its domain (the set of numbers the variable(s) can possibly be).
    Basically, denominators can not be zero and can not do square root of a negative number.
    Ex.    7x2-3x+4    x can be any/all real number
    Ex.    1/x    x can be any real number except 0
    Ex.    1/(x-2)2    x can be any real number except 2
    Ex.    (2x+1)/(2x2+2x-4)    x can be any real number except -2 and 1 (factor the denominator to see why)
    Ex.    √(3x+4)    x can be any real number ≥ -4/3.   [-4/3,∞)
    [Desmos: graph these as functions, y=, to see what can happen at numbers not in the domain.]

  3. optionally Simplify it by combining like terms, reducing fractions, and clearing parens, if needed or wanted e.g. to minimize subsequent evaluation or to clarify what's going on.
    Ex.    3x2-5x+4x2+2x+4 → 7x2-3x+4
    Ex.    3(x+2)-1-2(-4x+3) → 11x-1
    Ex.    3x2-5x   no like terms.

  4. Factor it, especially a polynomial, to break it down into smaller/est factors [simpler expressions] (pieces, components, building blocks).
    Ex.    7x2+3x-4 factors into (7x-4)(x+1)
    Ex.    3x3-75x factors into 3x(x-5)(x+5)
    Factoring can be difficult.

  5. Each side of an equation is an algebraic expression.
    LHS = RHS   
    You want to solve equations, i.e. find out what numbers when substituted into the variable(s) make a True equation, i.e. both sides evaluate to the same number.
    An equation is a logic statement; a logic statement is true or false. Equations are declarative sentences that are true or false.
    We want to know the Truths.
    Truth is where/when the good stuff, works, success, balances, clicks, copacetic, sweet spot, W.
    False is doesn't work, fails, lies, out-of-kilter, sour, kaput, zilch, L.

    Equations of one variable:    [have no graph]
    Linear equation of one variable. (x1 only)
    Solvable by doing same operations to both sides of the equation until reduces to x=number, the unique solution (usually). [Linear EQs of one variable are the only EQs that can be solved this way.]
    Ex.    3x+2 = 5x-1    → x = 3/2
         Substituting the solution 3/2 into the equation: 3(3/2)+2 = 5(3/2)-1 → 6.5 = 6.5, a True equation.
         Substituting every other number makes a false equation: e.g. x=1 → 3(1)+2 = 5(1)-1 → 5=4, False.
    Ex.    Rhind    x+x/4 = 15    → x = 12

    Quadratic equation of one variable. (has x2)
    Solvable [some by factoring, square root, completing the square. All by quadratic formula.] There will be 0, 1, or 2 [real number] solutions (but always two complex solutions).
    Ex.    7x2+2x+4 = 3x+12    → two solutions: x= 8/7 and -1    [can simplify if want to to: 7x2-x-8 = 0 "standard form"]
         Substituting 8/7 for x in both sides of the equation results in the True equation 15.428571=15.428571.
         Substituting -1 for x in both sides of the equation results in the True equation 9 = 9.
         Every other number results in a False equation.

    NB. an equation of one variable does not have a graph. [Desmos draws vertical lines at the x solutions.]
    Each side of the equation can be separately graphed as a function. The intersection points are the x solutions.

    Equations in two variables, say x and y.    [have graph]
    A solution is an x and y pair of numbers (x,y) that when substituted into the equation's expressions evaluates to a True equation.
    [Almost always] There is an infinite number of solutions.    [x2+y2=0 has only (0,0), x2+y2=-c has no solutions]
    The solutions can be graphed in the Cartesian rectangular XY coordinate plane, each point of the graph's curve being a solution to the equation. The graph is the set of all solutions, it is a "picture" of the equation's solution set.
    Equations of two variables can be graphed in Desmos.
    Ex.    3y2-x2 = 3x-2y   
         has an infinite number of solutions, (0,0), (0,-2/3), (-3,0) being three of them.
    Unless the equation is a function (see #6 below), can be hard to solve [but try setting each variable to 0].
    Exs.    x2-y2 = 2    x2+y2 = 2    y2-x2 = 2    x2 = y2
    Ex.    x2+y2+xy = 1
    Ex.    x2+(y-x2/3)2 = 1

    If the two-variable equation can be gotten into the form y = expression_in_x (i.e. isolate y) then that expression can be the definition of a function of x [see #6 below].
    [This "get into the form y=" is called "solving" for y; unfortunately the same word solve.]
    Ex.    12x-1+2y = 16x-3    can be solved for y:    y = 2x-1
    Ex.    y3-x2 = 3x+2    can be solved for y:    y = ∛(x2+3x+2)
    Ex.    3y2-x2 = 3x-2y    can NOT be solved for y. So cannot be a function.
         yeven term, but also sometimes only multiple odd-powered y's, eg. y3-y+x=0

    A formula is a "well-known" equation:
    A = ½bh
    C = 5/9(F-32)
    A = 4πr2
    V = 4/3 πr3
    A = P(1+r/n)nt
    E = mc2
    A = PB    [amount = percentage of the base]
    A formula expresses a relationship between quantities, allowing you to calculate one variable when the others are known.
    Formula can be rearranged to "solve" for any of its variables.
    Ex.    A = PB   ↔   B = A/P   ↔   P = A/B   ↔   A = PB
    Ex.    E = mc2   ↔   m = E/c2   ↔   c = √(E/m)

  6. An algebraic expression can be the definition of a function.
    Ex.    ƒ(x) = 2x-1,    a linear function.
    Ex.    ƒ(x) = 7x2+3x+4,    a quadratic function.
    Ex.    ƒ(x) = ∛(x2+3x+2),    the above example.
    (These function definitions use = but they aren't really equations. Some other symbol would be better...)

    A function can be evaluated for different values of the variable (x inputs), resulting in the value of the function (y outputs). The graph of the function is the set of these (x,y) pairs (typically an infinite number of them).
    The function values ƒ(x) are the y's, so y=ƒ(x).
    A function is a restricted equation of the form y = one_expression_in_x

  7. Each side of an inequality is an algebraic expression.
    Ex.    7x2+2x+4 ≤ 3x+12
    An inequality can be solved, i.e. what values when substituted into the variable(s) yields Truth. Typically an inequality's solution set is an interval; the example's solution set is: −1≤x≤8/7, or [-1,8/7], or graphically:

Algebra: why do?
--quantitative reasoning with quantitative information.
--real-world application (science, technology, engineering, economics, business, finance, statistics, ...).
--problem-solving skills training/improvement (logical thinking, pattern recognition, breaking complex problems into steps, perseverance)
--because it is there, to be discovered. (initially by mathematicians, now by you).
--gateway to higher math and thus more of the above