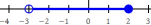Inequalities

P1.1: Solving a simple linear inequality is similar to solving a linear equation. "Isolate" the variable on one side of the inequality.
Ex.
3(x-1) + 2x < 6x + 3 simplifies to x>-6 so has solution {x|x>-6} or (-6,∞) or graphed on the real number line
Usually the solution set is an interval (e.g. x≤b (-∞,b] or x>b (b,∞) etc.) or is the empty set ∅ (if the inequality simplifies to 0<0 or x<x).

NB. multiplying or dividing both sides by a negative number requires the inequality sign to flip:
If a<b and c<0 then ac>bc

"at least" is ≥
"at most" is ≤   as is "no more than"

P2.5: Compound inequality with AND (conjunction):
Ex.
  3x+2>-7   AND   4x+1≤9     Solve each separately.
        x>-3     AND      x≤2
Solution set is the intersection ∩ of the solution sets of the two inequalities:
  -3<x≤2     (-3,2]    
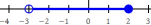
The solution is "sandwiched" in this interval.

"Three-part" inequality with the variable in the "middle" is actually a conjunction but can solve by doing same operation to all three "sides":
Ex.
-3 < -4x+1 < 13
Simplifies to: -3 < x < 1    (-3,1)   

"Three-part" inequality is an AND compound inequality:   a < x < b   ⇆   a < x AND x < b
If the variable is not in the "middle", need to "split" into two inequalities and solve each separately:
Ex.
2x-1 ≤ 4-x <6x+1    Split into two inequalities:
2x-1 ≤ 4-x    AND    4-x<6x+1     Solve each separately:
   x ≤ 5/3      AND    3/7<x   
   3/7<x ≤ 5/3    (3/7,5/3]   

Compound inequality with OR (disjunction):
Solve each inequality. Solution set is the union ∪ of the two solution sets.
Ex.
3x-5<-2 OR 4-5x≤-16     Solve each separately:
x<1 OR x≥4     Form the union ∪ of these:
(∞,1) ∪ [4,∞)   

An AND compound inequality's solution set can be ∅ and cannot be R.
Ex.   x≤3 AND x≥4    Solution is ∅

An OR compound inequality's solution set cannot be ∅ and can be R.
Ex.   x≤3 OR x≥2    Solution is (-∞,∞)

Mathpapa understands AND and OR.
It can also do the three-part variable-in-the-middle inequalities.

Absolute value ||

Equations:        (u is algebraic expression)
c>0, |u| = c → u=±c
   |u|=5 → u=5 or u=-5
   |2x+1|-6=3 → Isolate abs val: |2x+1|=9, then 2x+1=9 and 2x+1=-9, so x=4 and -5
|u| = -c → No solution ∅.
   |u|=-5 → ∅.

Inequalities:
c>0, |u|<c → -c<u<c
   |u|<5 → -5<u<5
   |2x+1|<5 → -5<2x+1<5 → -3<x<2   (-3,2)
c<0, |u|<c → No solutions ∅.
   |u|<-5 → ∅.

c>0, |u|>c → u<-c OR u>c
   |u|>5 → u<-5 OR u>5
   |2x+1|>5 → 2x+1<-5 OR 2x+1>5 → x<-3 OR x>2   (-∞,-3)∪(2,∞)
c<0, |u|>c → All real numbers ℝ
   |u|>-5 → ℝ

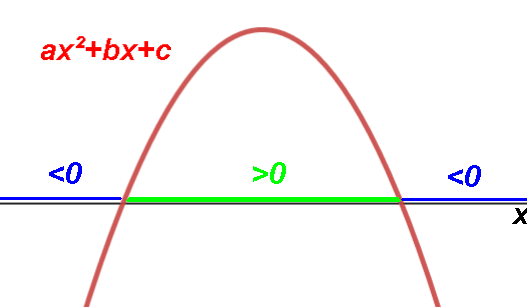
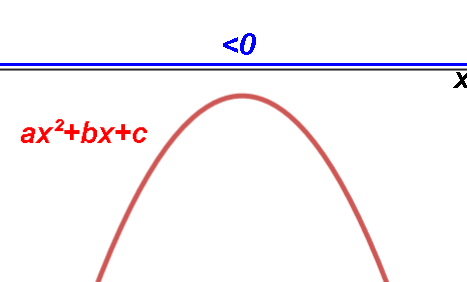
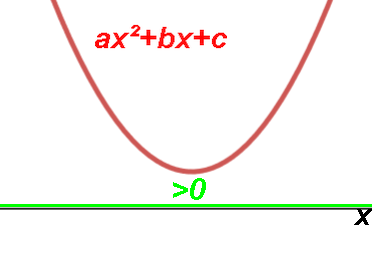
Quadratic inequalities.