
Uniform distribution: every value in range [a,b] equally likely.
mean=(a+b)/2 ie. =midrange=median
standard deviation SD = (b-a)/√12 ≈ (b-a)/3.464
~57.75% of data within 1 SD of mean, all is within 2 SD of mean.
MAD=range/4 Avg.diff.pair=range/3 ?
skew: 0
CDF(x)=P[X≤x]= (x-a)/(b-a)
Quantile InverseCDF Q(p)= p(b-a)+a =x
1-D uniform data distribution.

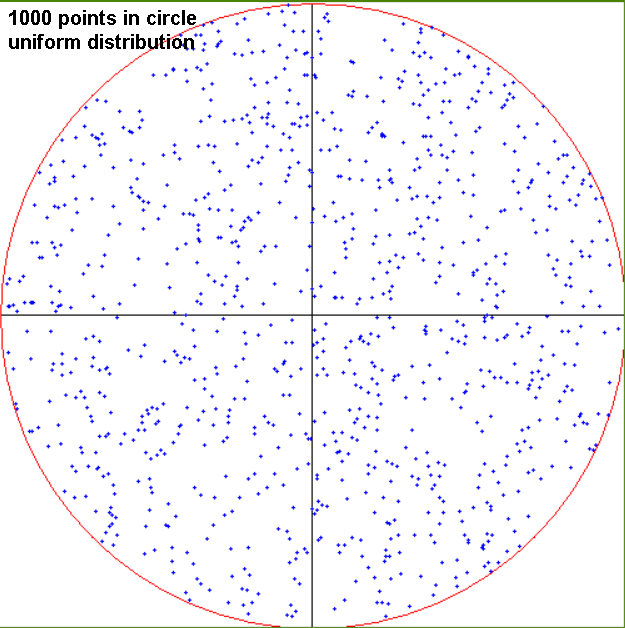
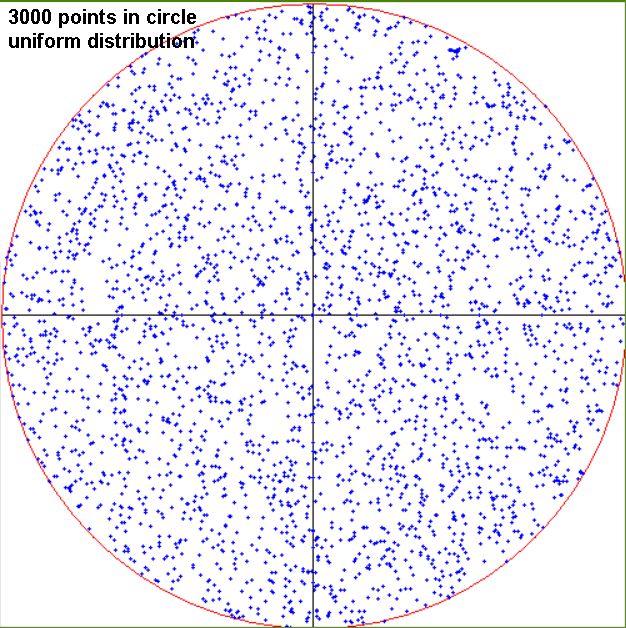
2-D uniform data distribution.
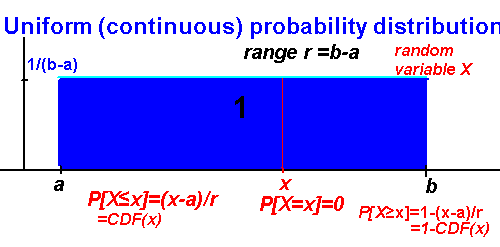
PDF (probability density function) is horizontal line at y= 1/(b-a).
Probability of any particular x value c is 0 (because continuous has infinite number
of values in the range). P(c)=0
CDF (cumulative density function) is area under the horizontal line.
All of the rectangle is all of the probability, so the area is 1 (i.e. 100% of the probability).
CDF is geometry, area of (sub)rectangle from a to c. P(X≤c) = (c-a)/(b-a)
Height of rectangle is 1/(b-a). Length is c-a. Height*Length=1/(b-a) * (c-a)
Special case when range starts at 0 (i.e. a=0).
CDF is geometry, area of rectangle from 0 to c. P(X≤c) = c/b
Height of rectangle is 1/b. Length is c. Height*Length=c/b

Ex. b=10, c=7 --> CDF(7)=P(X≤7)=7/10=.7 P(X≥7)=1-CDF(7)=1-.7=.3
c=7.2 --> CDF(7.2)=P(X≤7.2)=7.2/10=.72 P(X≥7.2)=1-CDF(7.2)=1-.72=.28
c2=4.9 --> P(4.9≤X≤7.2)=CDF(7.2)-CDF(4.9)=...=.72-.49=.33
The inequalities ≤ and ≥ can be < and >, it won't make any difference.