Poisson distribution probability

The number of times an event occurs in an interval of time or space or set of people.
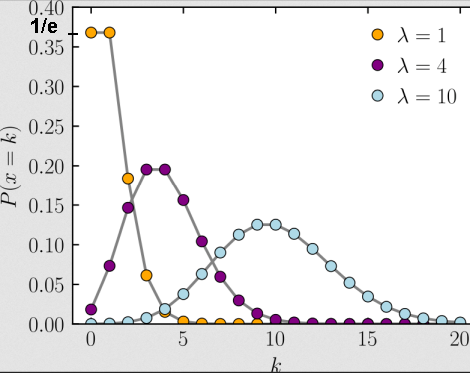
Probability of k events/arrivals occuring in an interval given λ the expected/mean number of random independent events that occur in an interval.
The sample space S = {0,1,2,...} i.e. the number of events/arrivals; has no upper bound.
P(k) the probability that in the interval there will be k events / arrivals:
P(k)=

Piscatorial example: suppose λ=4 fish are caught on average in one hour. (There's nothing fishy about Poisson!)
What is the probability of catching k=0 fish, k=1 fish, k=2 fishes, k=3 fishes, etc. in one hour?
Ex.: suppose λ=3 things exist in one cubic meter of some stuff.
What is the probability of observing k=0, 1, 2, 3, 4, 5, 6, etc. things in that cubic meter of stuff?
Ex.: Prussian Army soldiers killed by (accidental) horsekick (mules too?) was 0.61 per year (per cavalry corps).
What is the probability that no soldiers were horsekicked to death in a year, 1 soldier killed, 2, 3, 4 etc.?
Ex.: Tik Tok clicks occur 5.5 times per microsecond.
What's the chance that more than 7 occur in the next microsecond? ...

Expected/mean number of events in an interval (λ):   λ∈[0,∞)

mean= λ:
standard deviation= √λ:

   k        P(k)    ∑P(k)=CDF=P(≤k)   P(≥k)

The table continues up to 2*λ or as long as the probabilty is greater than .001.

Show a particular k:   
PMF(k) = P(k)=    CDF(k) is ∑P(k)=    P(≥k)=1-CDF(k-1)=

Probability histogram:

When λ is an integer, P(λ) = P(λ-1)

In 1/m of the interval, the expected/mean number of random independent events that occur in it is λ/m.
In m intervals, the expected/mean number of random independent events that occur in it is mλ.

P(0) = e^-λ
P(1) = λe^-λ

Binomial probability distribution can be approximated by the Poisson probability distribution with λ=np.

As λ gets larger, the pmf functions becomes Normalish:

Excel: Poisson.Dist(k, λ, TRUE/FALSE) FALSE for PMF, TRUE for CDF.