Chi-squared Χ2 test of goodness-of-fit (GOF)

See whether a frequency distribution fits, or conforms to, a particular distribution (a specific pattern).
Applied to categorical data to evaluate how likely it is that differences between the actual observed data and its expected/theoretical values arose by chance.
It tests a null hypothesis that the frequency distribution of certain events observed in a sample is consistent with a particular theoretical distribution. I.e. the observed distribution does not differ significantly from the expected distribution.
The events must be mutually exclusive and have total probability 1.
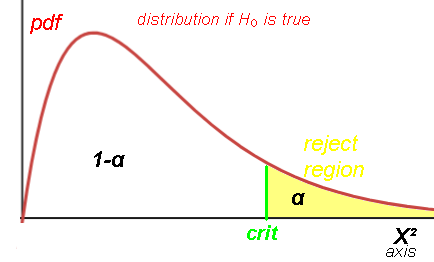
Are the differences between the sample's frequencies and the theoretical frequencies significant? (if so, reject H0). Or are the differences just due to random chance? (so fail to reject H0).

Observed frequencies Oi:
Expected frequencies Ei: (AKA Theoretical values) All should be ≥5.

Select a desired level of confidence (significance level, 1-α level) for the result of the test:

0.90 0.95 0.975 0.99 0.999

p: Theoretical distribution's number of parameters; reduction in df. (usually 1, but 3 for Normal, 2 for Poisson)

ΣOi=N=      #of categories:
degrees of freedom df= the number of categories reduced by the number of parameters of the fitted distribution, i.e. n-p degrees of freedom, where n is the number of categories, p the number of parameters.
   Resembles a normalized sum of squared deviations between observed and theoretical frequencies. Asymptotically approaches a Χ2 distribution.

Χ2 statistic=      critical value=      p_value:
If Χ2 test statistic > critical value, then reject the null hypothesis (H0 that there is no difference between the distributions, i.e. that it is a good fit), and the alternative hypothesis (HA that there is a difference between the distributions, i.e. that it is not a good fit) is supported, at the selected level of confidence; informally, the observed data does not fit the expected distribution, they are far apart. Χ2 is big and p_value low, the null must go.
If Χ2 test statistic < critical value, then, informally, the observed data does fit the expected distribution, they are close. Formally, there is insufficient evidence to conclude the observations do not fit the theoretical. Χ2 is small and p_value is big.
Χ2 test statistic is a measure of the discrepancy between Observed and Expected frequencies. The worse the fit, the larger is Χ2.
p_value is the area to the right of the Χ2 test statistic. Chance of a difference at least this large purely due to randomness.

The non-uniform Ei examples can be visualized in Visualize Two Dependent Samples
Roughly, if it's all/mostly vertical lines, it fits.

Excel: Line chart w/marker
category Oi Ei 

video. die 30 rolls:
#1s #2s #3s #4s #5s #6s
 3   3   4   8   7   5
Expected uniform distro: 1/6*30
 5   5   5   5   5   5

book: 45 die rolls:
13   6  12   9   3  2
Expected uniform distro: 1/6*45
7.5 7.5 7.5 7.5 7.5 7.5 

book: loaded die 45 rolls. 1 50%, 2-6 10%
13    6   12   9   3  2
22.5 4.5 4.5 4.5 4.5 4.5 

2 dice sum
      2         3       4      5 6 7 8 9 10 11 12
E= .027777  .055555  .083333 .111111 .1388888 .16666666 .1388888 .111111 .083333 .055555 .027777
n=100
Ei= 2.7777 5.5555 8.3333 11.1111 13.88888 16.666666 13.88888 11.1111 8.3333 5.5555 2.7777
Oi= 2       5      6     17      12       16        13        9      13      7      0      
Oi= 5      3      7      17      9        11        10       12      14      7      5     

last digit of self-reported weights  n=2784
1175 44 169 111 112 731 96 110 171 65
every E= 1/10*2784= 278.4  Expected uniform distro

Benford's law E
.301 .176 .125 .097 .079 .067 .058 .051 .046

Leading digits packet interarrival time
69 40 42 26 25 16 16 17 20    =271
271*Ei:
81.571 47.696 33.875 26.287 21.409 18.157 15.718 13.821 12.466

76 62 29 33 19 27 28 21 22
95.417 55.792 39.625 30.749 25.043 21.239 18.386 16.167 14.582


V-1 hits. #of the 576 London regions with 0,1,2,3,4 hits of 535 hits
229 211 93 35 8
227.5 211.4 97.9 30.5 8.7     expected Poisson u=.929

Kentucky Derby
19 14 11 15 16 7 9 12 5 11   =119
every E=119/10= 11.9

Old Faithful.  classwidth 10. Drop outlier 125   n=49
2 0 3 9 23 10 2
hmm, won't work on tails? <5   "can be combined with another class"
0.0029 0.0259 0.1165 0.2690 0.3191 0.1947 0.0610

Skittles colors   233 "of 4 bags"
Oi:   43 50 44 44 52
Ei:   46.6 46.6 46.6 46.6 46.6

The day-of-birth data in Nominal Data
n=400, each day equally likely, so Ei =400/7= 57.14 

Mendel's 556 pea seeds
% smooth-yellow smooth-green wrinkled-yellow wrinkled-green
Oi:  0.5666 0.1942 0.1816 0.0556
Ei:  0.5625 0.1875 0.1875 0.0625
*556:
315.0 108.0 101.0 30.9
312.7 104.2 104.2 34.8
Fisher said : BS, too good to be true

MLB birthdates months Jan-Dec:    4515
387 329 366 344 336 313 313 503 421 434 398 371
376.25 376.25 376.25 376.25 376.25 376.25 376.25 376.25 376.25 376.25 376.25 376.25

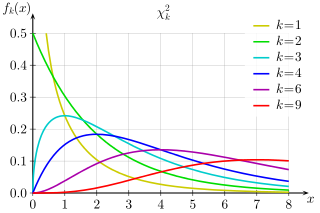
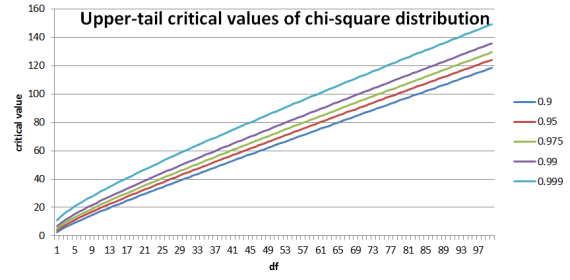
PDFs of chi-squared functions for first few values of df (k):

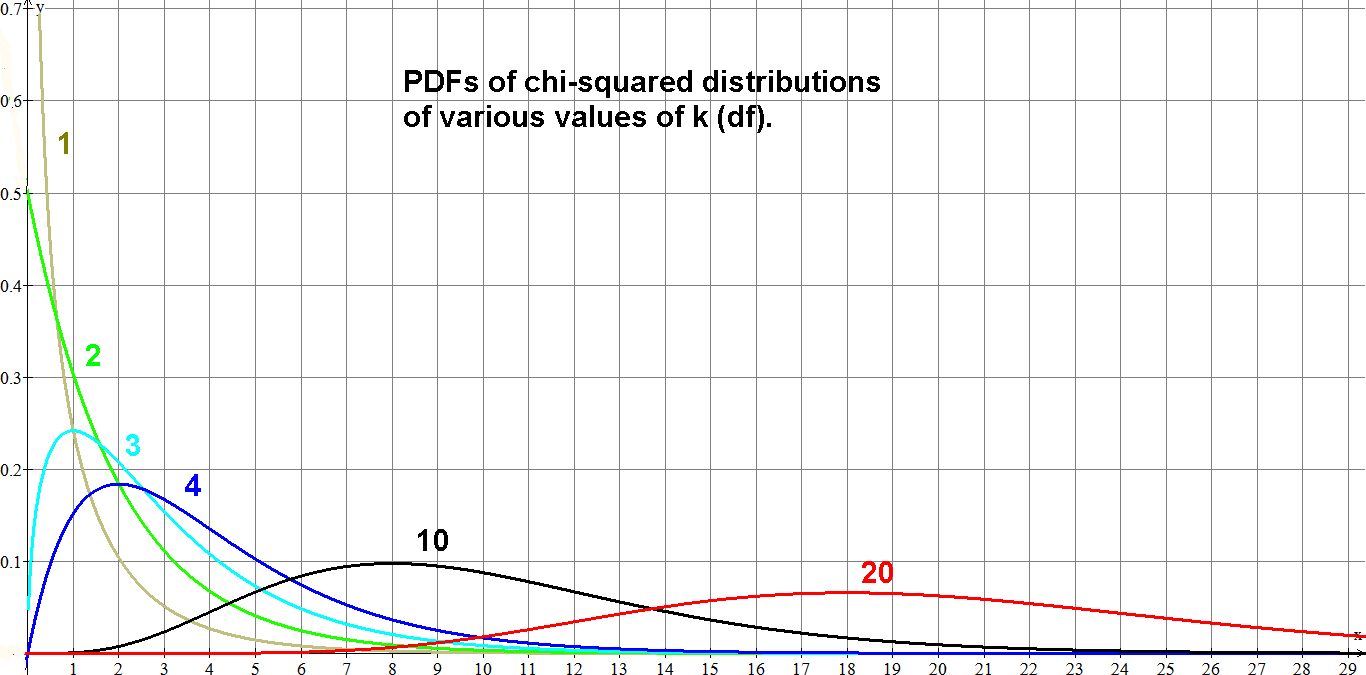
Area under each curve is 1 (is a probability distro). Small df: right-skewed; large df: becomes symmetric and bell-shaped.
df=1,2: peak at 0. df≥3: peak at df-2.

Sum of k squared random selections from the standard normal distribution.
Expected value of Χ2k = k
Variance of Χ2k = 2k

PDFs of chi-squared functions for various values of k:

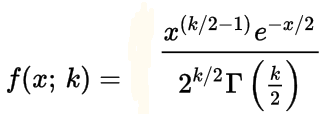Γ gamma function

k Γ(k/2) =/≈
1 Γ(1/2) 1.7724
2 Γ(1) 1
3 Γ(3/2) .8862
4 Γ(2)=1! 1
5 Γ(5/2) 1.3293
6 Γ(3)=2! 2
7 Γ(7/2) 3.3233
8 Γ(4)=3! 6
9 Γ(9/2)
10 Γ(5)=4! 24
20 Γ(10)9! 362880 

Mathpapa k= 1, 2, 3
y=\frac{x^{\left(\frac{1}{2}-1\right)}e^{-\frac{x}{2}}}{2^{\frac{1}{2}}\cdot 1.7724}\ \ ;\ \ \ \ y=\frac{x^{\left(\frac{2}{2}-1\right)}e^{-\frac{x}{2}}}{2^{\frac{2}{2}}}\ ;y=\frac{x^{\left(\frac{3}{2}-1\right)}e^{-\frac{x}{2}}}{2^{\frac{3}{2}}\cdot .8862}