Example:
in set notation: {(2,3),(-2.345,0),(2,5),(π,e)} The same 'x' can be used many times
(unlike a function where an 'x' can occur only once).
graphically:
Example:
Any region on the plane is a relation (an (infinite) set of points, the red ones)
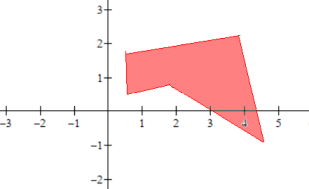
Example:
graph of the equation x3+y2-4x+2y-1=0
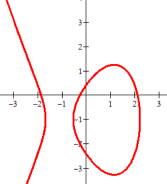
Is a (infinite) set of points (the red ones), so is a relation.
(Every "graph"/curve is a relation.)
(This relation is not a function because it obviously fails the vertical line test.)
The graph of an equation is the solution set, i.e. the points which when
substituted for the two variables results in a true statement.
Each of the equation, its graph, and the set of points is the relation between the two variables.
Every equation of two variables has a graph that is a relation. Some equations are functions, i.e. those that can be written as y = some function of x, i.e. y=ƒ(x). (Almost. There are some functions that can not (easily or using elementary operations only) be written that way, but we won't be seeing any of them. e.g. ey+y=x)
A function is a (restricted/special) relation. Not every relation is a function.
{functions} ⊂ {relations}
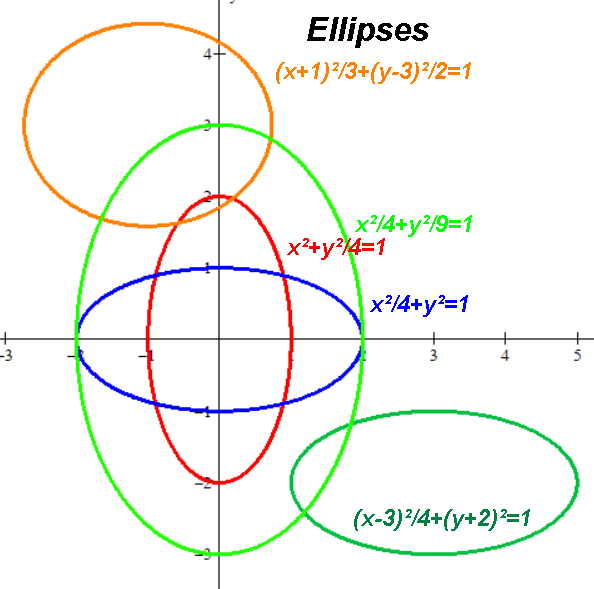
Algebra deals mostly with functions, not so much with relations (except for conic sections (circles, ellipses, hyperbolas, and parabolas) and pretty curves). Because the world is "functional", e.g. at time x an object is at one y place, or has one y speed, or is worth one y amount of money
The kawaii relation:
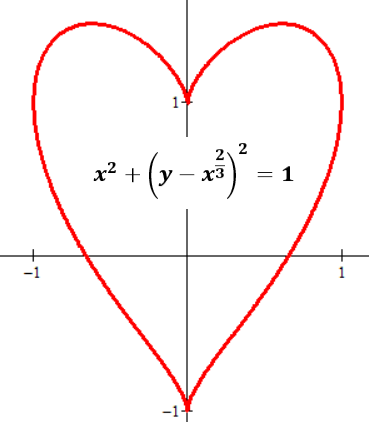
With love, from x and y.
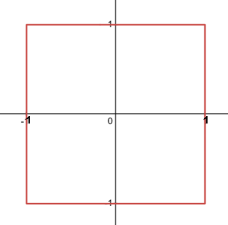
Square: centered at (h,k) with side length r: |(x-h)+(y-k)|+|(x-h)-(y-k)|=r
Unit square:
|x+y|+|x-y|=2
The Cartesian product of two sets is the set of all ordered pairs of the elements
of the two sets.
Example: if set one S1={a,b} and set two S2={1,2,3},
then their Cartesian product is:
S1 × S2 = {(a,1),(a,2),(a,3),(b,1),(b,2),(b,3)}.
Cartesian product is a set operation, like union and intersection are.
If the sizes of the two sets are n and m,
then the size of their Cartesian product is nm.
A relation is any subset of the Cartesian product of two sets.
Example relations between the two above sets: {(a,2),(a,3),(b,1)}, {(a,2),(b,2)}, {(b,1),(b,2),(b,3)},
{(a,1)}, ...
If the sizes of the two finite sets are n and m,
then there are 2nm relations between them.
In algebra, the two sets are most often ℝ, the set of real numbers,
or some subset of it (e.g. non-negative numbers).
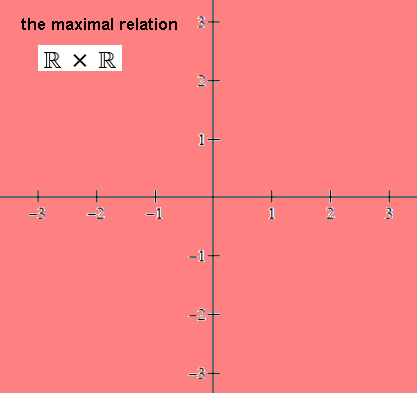
For two real-valued variables, the Cartesian product
is ℝ × ℝ = {(x,y)| x∈ℝ, y∈ℝ}
any tautology, e.g. 1=1, 2x=2x
any contradiction, e.g. 0=1, x=x+1, 2x+y=2x+y+1
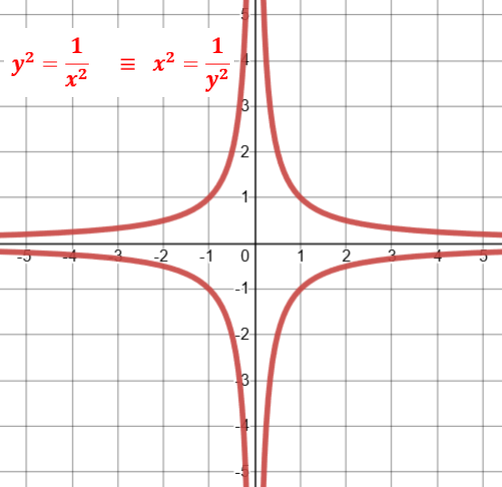
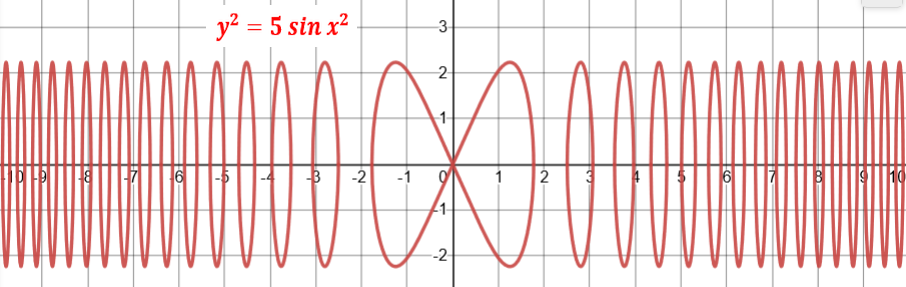
Every subset of these "objects" is a relation:
Named curves
Folium of Descartes:
x3 + y3 -3xy = 0
Kampyle of Eudoxus
x4 = x2 + y2
Tschirnhausen cubic
y2 = x3 + 3x2
Crooked egg
(x2 + y2)2 = x3 + y3
Cardiod:
(x2 + y2 - x)2 = x2 + y2