[3 different x coords, else can not be a function] and [non-collinear, i.e. not horizontal].
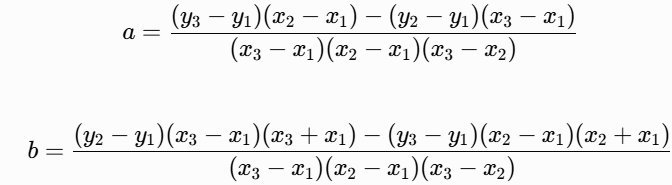 c by plugging any point back in: c = y1 - ax12 - bx1
c by plugging any point back in: c = y1 - ax12 - bx1


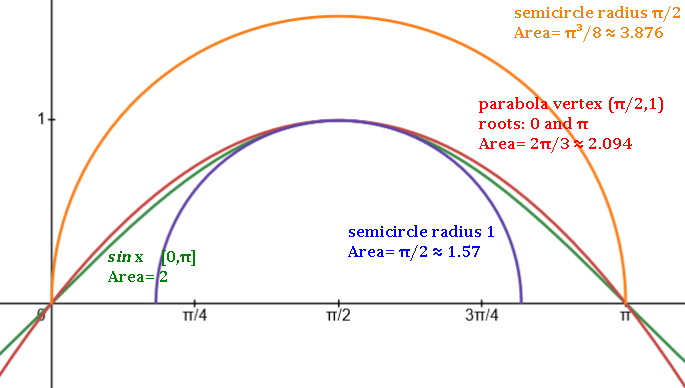
Parabola with vertex (0,k) on y-axis, with x-intercepts ±r:
y = -k/r2 x2 + k
Parabola with x-intercepts (zeroes) z1, z2:
y = (x-z1)(x-z2) = x2 -(z1+z2)x + z1z2
And all multiples thereof.
3 points determine a unique quadratic/parabola.
[3 different x coords, else can not be a function] and [non-collinear, i.e. not horizontal].
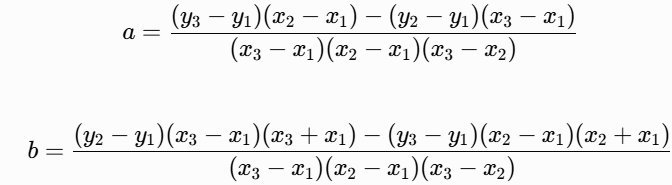 c by plugging any point back in: c = y1 - ax12 - bx1
c by plugging any point back in: c = y1 - ax12 - bx1

Free fall.
Distance fall pulled down by gravity, as a function of time.
d=1/2 gt2
t is seconds.
g is a constant factor, on Earth equal to 9.8 (metric) or 32 (American).
Gravity is an accelerating force: the speed (velocity) gets faster and faster.
The velocity at any time t = gt (i.e. a linear function of t).
Falling
Air resistance is ignored (i.e. not taken into consideration, as if Earth had no atmosphere).


Watch the hammer drop at 0:57
he's showing the effect of no air but it also shows the effect of the force of gravity on another world.
Go straight up, then fall straight down.
Height of an object shot straight up with different starting speeds, as a function of time.
h(t) = -1/2 gt2 + vot
vo is the initial velocity (e.g. muzzle velocity). So, a different function for every different initial velocity.
As usual, air resistance is ignored.

MPH*1.46 = ft/s 0.68*ft/s = MPH
NB. the curves are not the trajectory of the object (which goes straight up and down).
f(x)=ax2+bx+c Quadratic function.
f'(x)=2ax+b Derivative of quadratic function is linear.
Evaluated at x tells slope m of tangent line at (x,y); this slope is the
rate of change of the quadratic function at that point.
Ex. above height function of object fired straight up: h(t) = -1/2 gt2 + vot
(first) derivative h'(t) = -9.8t + vo is velocity of object at time t
second derivative h''(t) = -9.8 is acceleration of object at time t. constant acceleration of Earth's gravity.
y=(2ax1+b)x+(c-ax12)
Equation of tangent line at (x1,y1)









Wikipedia Other realworld parabolas