A subclass of polynomial function where the variable x is only in the first power
(i.e. a degree-one polynomial in one variable (i.e. univariate)).
m and b are any real numbers.
In polynomial-ish form: ƒ(x) = a1x1 + a0
All other functions are non-linear.
And/or equivalently, y = mx + b a linear equation of two variables.
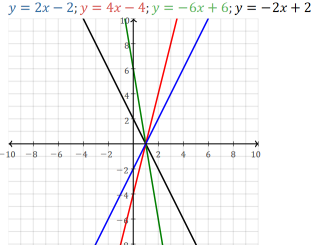
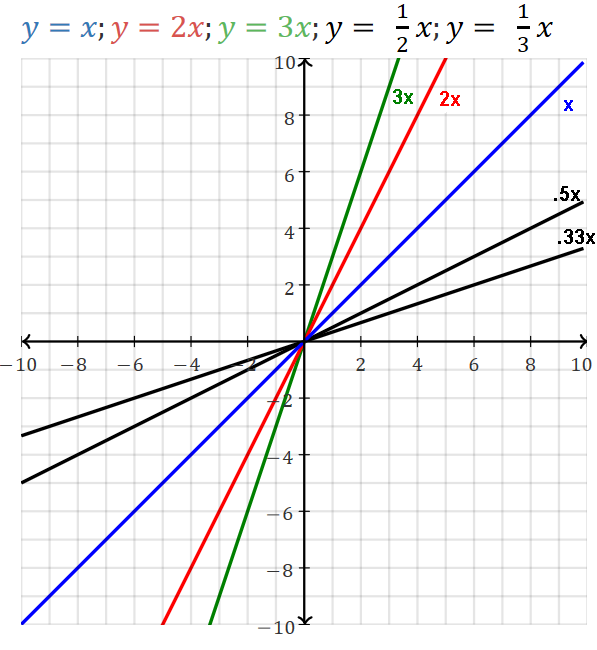
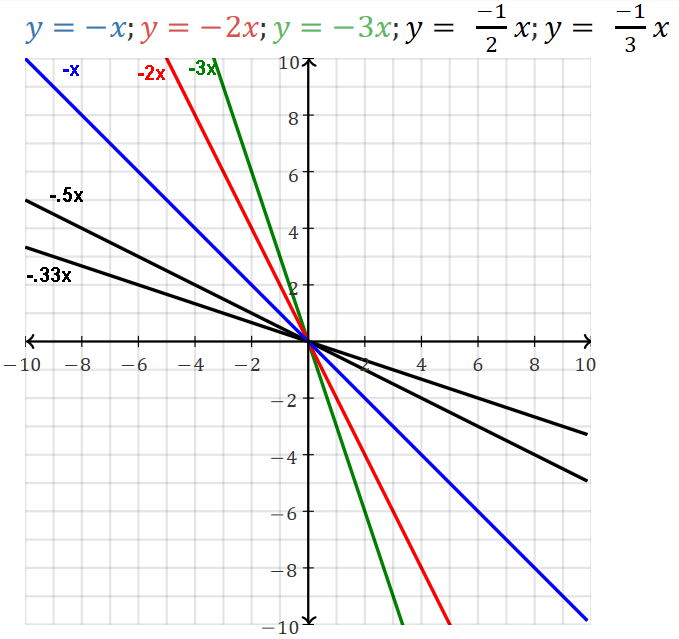
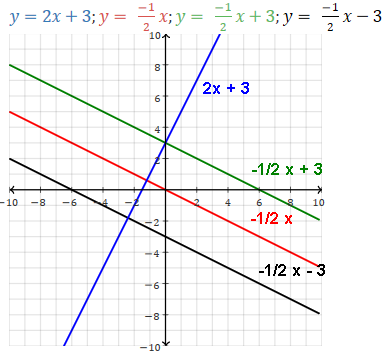
m is the slope.
b is the y-intercept.
Its graph in the xy Cartesian plane is a (straight) line.
This is why linear functions are called line-ar.
(A graph shows all the points (i.e. pairs of x and y values) that make the equation true.
And shows, for each value of x, its corresponding ƒ(x) (i.e. y) function value.)
Linear functions are the simplest functions; but very useful.
The domain of every linear function is R. The range is R too, except
for the special case of constant (horizontal) functions whose range is just one number.
Slope is the steepness/shallowness, grade, gradient, tilt, pitch, slant, incline/decline of the line.
The slope is the same at all points of the line.
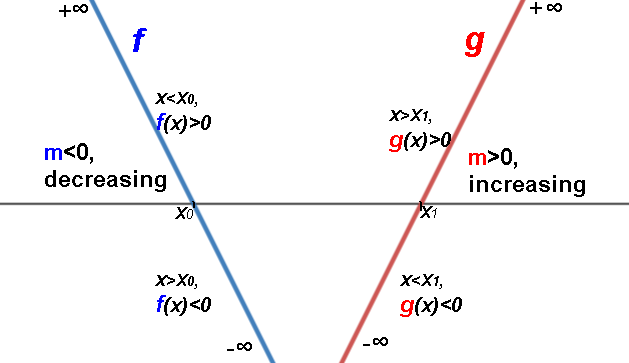
Slope is how much the function is increasing or decreasing,
i.e. its rate of change,
which is how much the real-world process/activity is changing.
A linear function's rate of change is unchanging, i.e. it is the same, it is a steady rate.
Linear means wherever the x is (e.g. near -∞ or +∞ or 0)
the change of y is the same for the same change of x.
Linear function as all multiples of m.
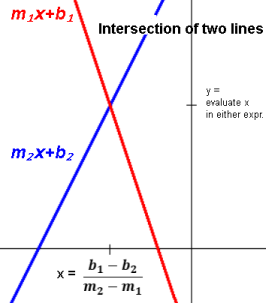
Between any two points:
--the rise over the run;
--the change in the vertical divided by the change in the horizontal;
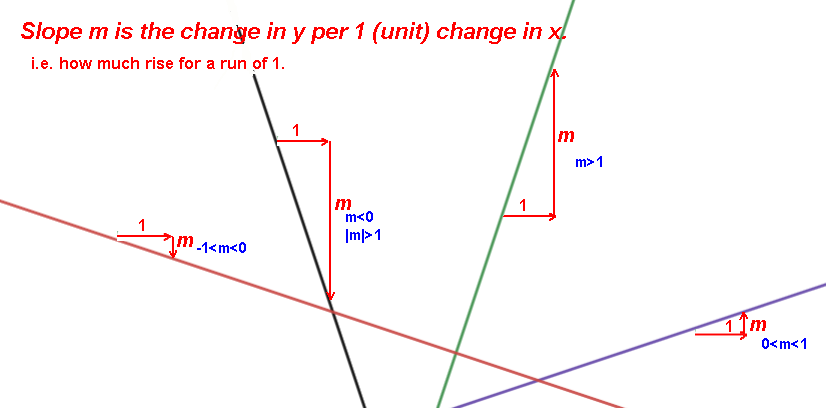
--the change in y per one unit change in x, i.e. the rate of change of the y,
the unit rate of y's per x.
--the change in y as a percentage of x: %=m*100% (e.g. y=2x y=200%x; y=1/2x y=50%x)
Ex. a slope of 2 means for a one unit increase of X the Y increases by 2.
Ex. a slope of -2 means for a one unit increase of X the Y decreases by 2.
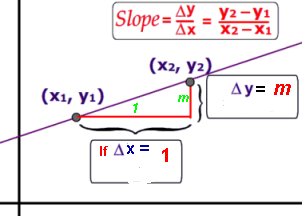
m = Δy / Δx
= (y2-y1)/(x2-x1)
= (y1-y2)/(x1-x2)
for every pair of points on the line.

Slope Explorer demos slope.
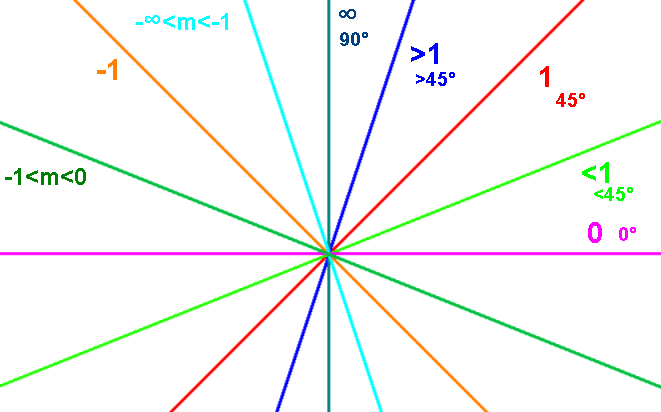
Slope is a kind of angle the line makes with the horizontal.
It is interconvertible to angle via trig functions:
If α is an angle in radians: m=tan(α) and m=tan(angle°*(π/180))
α=arctan(m) and angle°=arctan(m)*(180/π)
Exs. m=0.5 α=26.6°
m=1 α=45°
m=2 α=63.4°
m=3 α=71.6°
m=10 α=84.3°
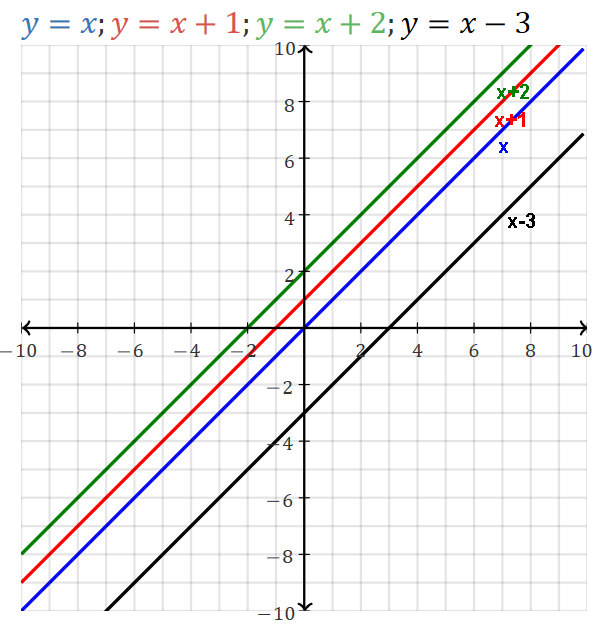
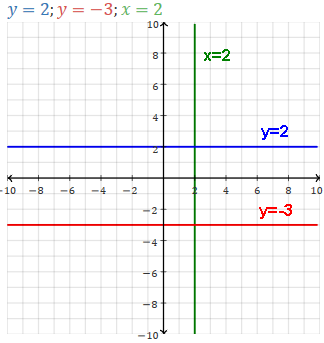
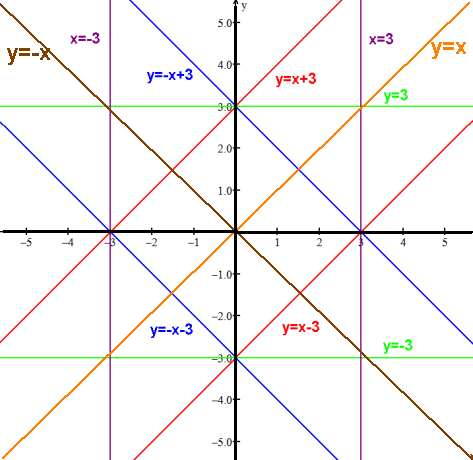
Line crosses the y axis at the y-intercept: (0,b).
If b is 0, graph crosses origin (0,0).
A nonzero b is an offset from the origin, often representing an initial value.
Line crosses the x axis at the x-intercept, also called the zero of the function: (-b/m,0).
X-intercept's x coordinate is the solution to the linear equation mx+b=0.

Every linear function's line crosses both axes.
(Except the special case of horizontal lines, see below).
One end goes up to +∞, the other goes down to -∞.
There are no extrema, turning points, inflection points.
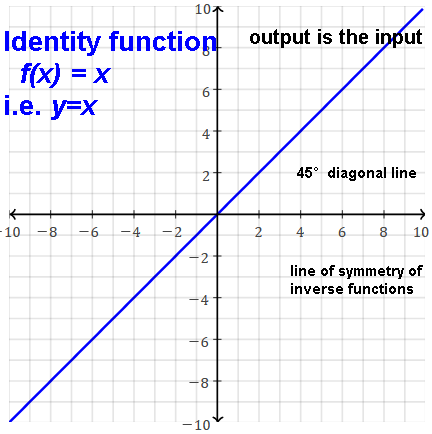
A line through the origin has x-intercept and y-intercept at the same point, i.e. (0,0).
A line through the origin is symmetric about the origin, i.e. an odd function.
I.e. ƒ(-x)= -ƒ(x) [m(-x)=-mx] and ƒ(x)= -ƒ(-x) [mx=-m(-x)].
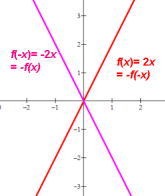
A line not through the origin is neither odd nor even.
All multiples of a linear function have the same x-intercept
(as all multiples of a linear equation have the same solution):