Uses:
--solve exponential equations.
--some scales are logarithmic: pH, decibels (sound), Richter earthquake (fury), star magnitude, Moore's Law. To accommodate the large ranges. A line represents exponential growth.
--log scale graph paper.    Elements    Earthquakes
--historical: ease some calculations (when no calculator): multiplication of large factors turned into addition of the logs of the factors, (division turned into subtraction of the logs of the dividend and divisor):
123456789*987654321 = log(123456789) + log(987654321)
≈8.09 + 8.98 = 17.07
10^17.07 ≈ 117,489,755,493,952,954
NB. log(117,489,755,493,952,954) ≈ 17.07
--Basis of the slide rule.
--List of logs: log tables at the back of textbooks.

log_b(x) = y, the exponent to raise b to to equal x:    b^y= x

log_b n = p, the power p to raise the base b to to equal the number n:    b^p= n
A logarithm (value) is an exponent. Convert a number to its exponent.
log₁₀ 1000 = 3, the exponent to raise 10 to to equal 1000: 10³= 1000
log₂ 32 = 5, the exponent to raise 2 to to equal 32: 2⁵= 32
log₂ 1/8 = -3, the exponent to raise 2 to to equal 1/8: 2^-3= 1/8

"log" is the name of the function/operation. Could say f(x)=log_b(x)
The parentheses are optional: log_b x    NB. log x + 3 ≠ log(x+3)
You "take" a logarithm, like you "take" a square root. Taking a logarithm is an operation on a number, like taking its square root is, or raising it to a power.
Unlike other functions (e.g. linear, quadratic, exponential, rational), a logarithm function doesn't have an algebraic expression involving +-*/²√ defining what it does. It does/means a certain operation on its argument. It doesn't have a symbol like √ or +-*/^p. cf. sqrt()
Logarithm is both an operation (log 9) and a function (f(x)=log x), like square root is (√9 and f(x)=√x).

b is the base, any/every positive real number: b>0. There are an infinite number of different logarithmic functions, one for every positive real number. But the two most common bases are 10 (common log: log without any base shown) and e (natural log: ln). Caveat: sometimes someplaces log means natural log (e.g. WolframAlpha, Python).
"logarithm" literally means something unhelpful like "ratio number"

Recall the powers of 10:
10⁰ = 1
10¹ = 10
10² = 100
10³ = 1000
10⁴ = 10000
log₁₀ x = y, the exponent to raise 10 to to equal x
log₁₀ 10000 = 4, the exponent to raise 10 to to equal 10000
log₁₀ 1000 = 3, the exponent to raise 10 to to equal 1000
log₁₀ 100 = 2, the exponent to raise 10 to to equal 100
log₁₀ 10 = 1, the exponent to raise 10 to to equal 10
log₁₀ 1 = 0, the exponent to raise 10 to to equal 1
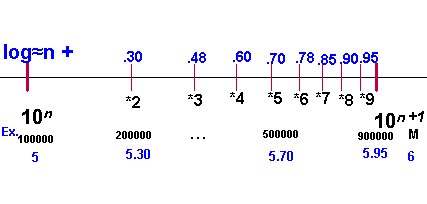
For positive powers of 10, the log function tells how many 0's it has.
Or is approximately how many digits a positive number has.
log₁₀ 0.1 = -1, the exponent to raise 10 to to equal 0.1=1/10=10^-1
log₁₀ 0.01 = -2, the exponent to raise 10 to to equal 0.01=1/100=10^-2

Recall the powers of 2:
2⁰ = 1
2¹ = 2
2² = 4
2³ = 8
2⁴ = 16
2⁵ = 32      Powers of 2 worksheet
log₂ x = y, the exponent to raise 2 to to equal x
log₂ 16 = 4, the exponent to raise 2 to to equal 16
log₂ 8 = 3, the exponent to raise 2 to to equal 8
log₂ 4 = 2, the exponent to raise 2 to to equal 4
log₂ 2 = 1, the exponent to raise 2 to to equal 2
log₂ 1 = 0, the exponent to raise 2 to to equal 1
log₂ 0.5 = -1, the exponent to raise 2 to to equal 0.5=1/2=2^-1
log₂ 0.25 = -2, the exponent to raise 2 to to equal 0.25=1/4=2^-2

Calculators have a log button (common log) and ln button (natural log). MathPapa knows log and ln. Use a calculator or software to evaluate a log. Some calculators have log_b button. Windows calculator: log_yx button. Desmos: Keypad | functions | Calculus | log_a OR log Shift- to get into base area.
log 500 = 2.69897..., the (irrational) exponent to raise 10 to to equal 500. 10^2.69897≈500
log 50 = 1.69897..., the (irrational) exponent to raise 10 to to equal 50
log 5 = 0.69897..., the (irrational) exponent to raise 10 to to equal 5
log 0.5 = -0.301029..., the (irrational) exponent to raise 10 to to equal 0.5
Log 2 worksheet

Natural log: ln The base is e     = log_e ≈ log_2.71828
We are not familiar with the powers of e... Use a calculator or software to evaluate a ln.
ln e² = 2, the exponent to raise e to to equal e² duh     e²≈7.3890561     ln 7.3890561≈2
ln e³ = 3, the exponent to raise e to to equal e³     e³≈20.085537     ln 20.085537≈3
ln 10≈2.3025851, the exponent to raise e to to equal 10.     e^2.3025851≈10
ln 100≈4.6051702, the exponent to raise e to to equal 100.     e^4.6051702≈100
ln 2≈0.6931, the exponent to raise e to to equal 2.     e^0.6931≈2
ln 1/2≈-0.6931, the exponent to raise e to to equal 1/2.     e^-0.6931≈1/2
"An artificial log is Duraflame."

Logarithmic functions are very slow growing.
NB. graph is not to scale:

Continuous and smooth. No wiggle, no extrema, no turning points.
Domain is (0,∞): no logs of negative numbers or 0. Range is R.
X-intercept at (1,0). Vertical asymptote is Y axis (x=0), so no y-intercept.
(b,1) is on the curve of f(x)=log_b x    as is (1/b,-1)
log_b a, where a<1, is negative. e.g. log 0.1=-1
NB. graph is not to scale:

Worksheet log and ln

General logarithmic functions: ƒ(x)= a·log_bkx + c     or expression
Ex. 2 log 3x - 4

log googol = 100     googol=10¹⁰⁰
log log googol = log² googol = 2
log log 10¹⁰ = 1
log log log googolplex = 2     googolplex=10^googol

log 1/x = - log x

Change of base formula.
log_b x = log_c x / log_c b    
Typically c is 10 or e: log_b x = log x / log b = ln x / ln b
log_old x = log_new x / log_new old
Useful if calculator can't do other logs (except common and natural).
Logs in different bases b and c differ by a constant factors log_bc and log_cb.
Ex. log₅ 100 = log 100 / log 5   = ln 100 / ln 5
Ex. log₂ 100 = log 100 / log 2   = ln 100 / ln 2
Convert log to ln by multiplying by ~2.3: ln x ≈ 2.3 log x
Convert ln to log by dividing by ~2.3 or multiplying by 1/2.3=.434: log x ≈ .343 ln x
log_b a = log_a a / log_a b = 1 / log_a b

"Laws"/facts/properties of logarithms: to manipulate log expressions, to "expand" or to "compactify" a log expression.

log_b b = 1      log_b 1/b = -1

Every log:
log 1 = 0

Power rule:
log xⁿ = n log x
     Exs. ln x⁴ = 4 ln x    ln 4^x = x ln 4    Special case: log(1/x)= log x^-1= - log x

Product rule:
log(xy) = log x + log y    log of a product equals the sum of the logs of the factors.
     Exs. ln 4x = ln 4 + ln x    log 20 + log 5 = log 100

Quotient rule:
log(x/y) = log x - log y    log of a quotient equals the difference of the logs.
     Exs. ln 4/x = ln 4 - ln x    log 100 - log 20 = log 5

Non-laws:
log(x+y)≠
log(x-y)≠
log(x)*log(y)≠
log(x)/log(y)≠

log_b b^x = x      ln e^x = x     logging an exponential leaves the exponent.
    Exs. log 10³=3    log₂ 2⁴ = 4    ln e⁵=5

b^{log_b x} = x      e^{ln x} = x     exponentiating a log leaves the log's argument.
    Exs. 10^{log 1000}=1000    2^log₂16=16    e^{ln e5}=e⁵

Exponent and logarithm are the inverse/reverse of each other, they "undo" what the other did. Logarithm is exponentiation "inside out".

10^x inverse is the common logarithm function: log x
b^x inverse is the logarithm base b function: log_b x
e^x inverse is the natural logarithm function: ln x

Like all inverse functions, they are reflections of each other over the y=x main diagonal.
e^x has horizontal asymptote X axis (y=0). ln x has vertical asymptote Y axis (x=0).
Domain of e^x is R. Range is (0,∞).
Domain of ln x is (0,∞). Range is R.

The exponential function, e^x, is sometimes denoted exp(x).
ln e^x = ln(exp(x)) = x
e^{ln x} = exp(ln(x)) = x

Solving exponential or logarithmic equations.
If have an exponential (i.e. x is in the exponent) equation, b^x = a
take logs of both sides (i.e. same operation to both sides), will "undo" the exponent:
 →  log_b b^x = log_b a
and then
EITHER    b^x = a → x = log_b a
Ex. 10^x=3.4567  →  log 10^x= log 3.4567  →  x = log 3.4567  →  x≈0.5386616
OR use the power property:  →  x log_b b = log_b a  →  x = log_b a    [ log_b b=1]
Ex. 10^x=3.4567  →  log 10^x= log 3.4567  →  x log 10 = log 3.4567  →  x≈0.5386616

If have a logarithmic (i.e. x is in a log) equation, log_b x = a
raise the base b to both sides (i.e. same operation to both sides), will "undo" the logarithm:
Exponent law/fact: b^log_ba = a    Exs. 10^{log 1000} [ = 10³ ] = 1000    10^{log 50} [ = 10^1.69897000 ] = 50    e^{ln 100} [ = e^4.605170186 ] = 100
log_b x = a  →  b^{log_b x} = b^a  →  x = b^a
Ex. log x=0.5386616  →  10^{log x} = 10^0.5386616  →  x = 3.456699
Beware the extraneous solution.

More

---

Derivative of ln: (ln x)' = 1/x
rate of change of ln x at x is 1/x
Integral of ln: ∫ln(x) = x ln(x)- x = x(ln x -1)

Derivative of log_b: (log _bx)' = 1 / (x ln b)
Derivative of general logarithm function: (a·log_bcx + d)' = a / (x ln b)
Integral of log_b: ∫log _bx = x(ln x - 1) / ln b
Integral of general logarithm function: ∫a·log_bcx + d = x(a ln cx - a + d ln b) / ln b

"Naturalness": slope of tangent line to ln(x) at (1,0) is 1.

b^x=e^ln(b)x     2^x=e^ln(2)x=e^.6931x     3^x=e^ln(3)x=e^1.098x
e^ax=(e^a)^x

Doubling time of continuous growth:
FV=Pe^rt     if FV=2P then     2P=Pe^rt    2=e^rt     ln 2 = rt

ln -2 = ln 2 + πi