Circle centered at origin has what symmetries?
Circle centered at origin (0,0) with r is the radius:


Circle centered at origin has what symmetries?
Circle centered at (h,k): using distance formula:
√((x-h)2+(y-k)2)=r
Standard form equation of a circle: can read off the center and radius.
Every such equation is a circle.
Radius r is size, (h,k) center is location.

Might have x and/or y intercept(s). For x intercepts, set y to 0 and solve for x.
For y intercepts, set x to 0 and solve for y. MP


Given the center and radius, can make the standard form equation.
Ex. Center (-5,2) radius 3: (x+5)2+(y-2)2=9
General form equation of a circle: x2+y2+Dx+Ey+F=0
x and y both squared, and with same coefficient, either both positive or both negative:
Ax2+Cy2+[Dx]+[Ey]+F=0, A=C
The general form relates circles to other conic section (ellipses, parabolas, hyperbolas)
quadratics.
Convert standard form to general form equation:
x2+y2-2hx-2ky+(h2+k2-r2)=0
Hint: MP simplify LHS expression
Convert general form to standard form: complete the square for each variable. Wolfram "Alternate form"
h = D/-2 k = E/-2 r = √(h2+k2-F)
Circumference = 2πr. d=2r, so C = πd
π=C/d the ratio of circumference to diameter [of every circle].
The circumference is a bit more than three times the length of the diameter.
The diameter is a bit less than one-third the circumference.
Area of a circle = πr2.
Squared units, so not directly comparable with length unit.
The area is a bit more than three times the area of a square whose side length is r.

Double the radius → double the circumference and quadruple the area.
Circle is the shape that encloses the most area for a given boundary. C=1 → A=1/(4π)≈0.079577 (cf. square of side 1/4 has area 1/16=.0625, equilateral triangle of side 1/3 has area √3/36≈.0481, isosceles right triangle of sides 1/(2+√2)≈.2929 and hypotenuse .√2/(2+√2)≈.4142 has area ≈ .0607)
Circle vs line: two ends of a spectrum?
Line: open-ended, to infinities, straight every point, same change rate
Circle: closed loop, bounded, curvy every point, (all) differing change rates
Semicircle functions.
upper half of circle centered at origin with radius r: f(x) = √(r2-x2)
lower half of circle centered at origin with radius r: f(x) = -√(r2-x2)

upper/lower semicircles centered at (h,k) with radius r: f(x) = ±√(r2-(x-h)2) + k

Disc
Centered at (h,k) with radius r:
(x-h)2+(y-k)2 ≤ r2
Closed disc includes the circle: ≤
Open disc excludes the circle: <
"Unit disc": x2+y2 ≤ 1

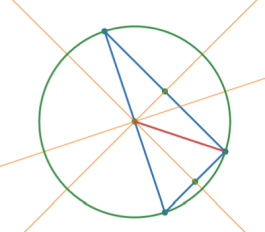
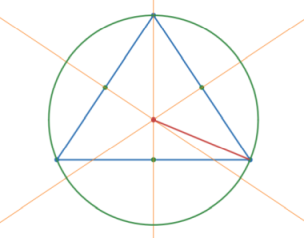
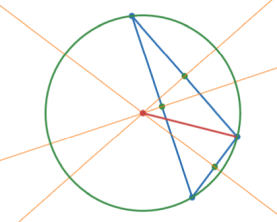
Three non-collinear points define a circle.
whose center is the circumcenter of the triangle defined by the 3 points.
Circumcenter of: 1. right triangle is midpoint of hypotenuse;
2. acute triangle is interior; 3. obtuse triangle is exterior.
Circumcenter is the intersection of the perpendicular bisectors of the triangle's sides.
Archimedes: area of circle equals area of triangle whose base is C and height is r.

Intersecting circles
Equation of line through the two intersection points:
y = (h1-h2)/(k2-k1)x +
(h22+k22-r22-
h12-k12+r12)/
(-2k1+2k2)