Chi-squared Χ2 test of goodness-of-fit
applied to categorical data to evaluate how likely it is
that differences between the actual observed data
and its expected/theoretical values arose by chance.
It tests a null hypothesis that the frequency distribution of certain
events observed in a sample is consistent with a particular theoretical distribution.
The events must be mutually exclusive and have total probability 1.
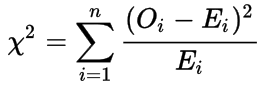
Resembles a normalized sum of squared deviations between observed and theoretical frequencies.
Asymptotically approaches a Χ2 distribution.
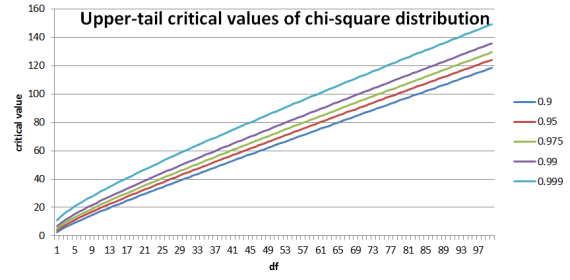
Upper-tail critical values of chi-square distribution.
df Probability less than the critical value
0.90 0.95 0.975 0.99 0.999
1 2.706 3.841 5.024 6.635 10.828
2 4.605 5.991 7.378 9.210 13.816
3 6.251 7.815 9.348 11.345 16.266
4 7.779 9.488 11.143 13.277 18.467
5 9.236 11.070 12.833 15.086 20.515
6 10.645 12.592 14.449 16.812 22.458
7 12.017 14.067 16.013 18.475 24.322
8 13.362 15.507 17.535 20.090 26.125
9 14.684 16.919 19.023 21.666 27.877
10 15.987 18.307 20.483 23.209 29.588
11 17.275 19.675 21.920 24.725 31.264
12 18.549 21.026 23.337 26.217 32.910
13 19.812 22.362 24.736 27.688 34.528
14 21.064 23.685 26.119 29.141 36.123
15 22.307 24.996 27.488 30.578 37.697
16 23.542 26.296 28.845 32.000 39.252
17 24.769 27.587 30.191 33.409 40.790
18 25.989 28.869 31.526 34.805 42.312
19 27.204 30.144 32.852 36.191 43.820
20 28.412 31.410 34.170 37.566 45.315
21 29.615 32.671 35.479 38.932 46.797
22 30.813 33.924 36.781 40.289 48.268
23 32.007 35.172 38.076 41.638 49.728
24 33.196 36.415 39.364 42.980 51.179
25 34.382 37.652 40.646 44.314 52.620
26 35.563 38.885 41.923 45.642 54.052
27 36.741 40.113 43.195 46.963 55.476
28 37.916 41.337 44.461 48.278 56.892
29 39.087 42.557 45.722 49.588 58.301
30 40.256 43.773 46.979 50.892 59.703
31 41.422 44.985 48.232 52.191 61.098
32 42.585 46.194 49.480 53.486 62.487
33 43.745 47.400 50.725 54.776 63.870
34 44.903 48.602 51.966 56.061 65.247
35 46.059 49.802 53.203 57.342 66.619
36 47.212 50.998 54.437 58.619 67.985
37 48.363 52.192 55.668 59.893 69.347
38 49.513 53.384 56.896 61.162 70.703
39 50.660 54.572 58.120 62.428 72.055
40 51.805 55.758 59.342 63.691 73.402
41 52.949 56.942 60.561 64.950 74.745
42 54.090 58.124 61.777 66.206 76.084
43 55.230 59.304 62.990 67.459 77.419
44 56.369 60.481 64.201 68.710 78.750
45 57.505 61.656 65.410 69.957 80.077
46 58.641 62.830 66.617 71.201 81.400
47 59.774 64.001 67.821 72.443 82.720
48 60.907 65.171 69.023 73.683 84.037
49 62.038 66.339 70.222 74.919 85.351
50 63.167 67.505 71.420 76.154 86.661
51 64.295 68.669 72.616 77.386 87.968
52 65.422 69.832 73.810 78.616 89.272
53 66.548 70.993 75.002 79.843 90.573
54 67.673 72.153 76.192 81.069 91.872
55 68.796 73.311 77.380 82.292 93.168
56 69.919 74.468 78.567 83.513 94.461
57 71.040 75.624 79.752 84.733 95.751
58 72.160 76.778 80.936 85.950 97.039
59 73.279 77.931 82.117 87.166 98.324
60 74.397 79.082 83.298 88.379 99.607
61 75.514 80.232 84.476 89.591 100.888
62 76.630 81.381 85.654 90.802 102.166
63 77.745 82.529 86.830 92.010 103.442
64 78.860 83.675 88.004 93.217 104.716
65 79.973 84.821 89.177 94.422 105.988
66 81.085 85.965 90.349 95.626 107.258
67 82.197 87.108 91.519 96.828 108.526
68 83.308 88.250 92.689 98.028 109.791
69 84.418 89.391 93.856 99.228 111.055
70 85.527 90.531 95.023 100.425 112.317
71 86.635 91.670 96.189 101.621 113.577
72 87.743 92.808 97.353 102.816 114.835
73 88.850 93.945 98.516 104.010 116.092
74 89.956 95.081 99.678 105.202 117.346
75 91.061 96.217 100.839 106.393 118.599
76 92.166 97.351 101.999 107.583 119.850
77 93.270 98.484 103.158 108.771 121.100
78 94.374 99.617 104.316 109.958 122.348
79 95.476 100.749 105.473 111.144 123.594
80 96.578 101.879 106.629 112.329 124.839
81 97.680 103.010 107.783 113.512 126.083
82 98.780 104.139 108.937 114.695 127.324
83 99.880 105.267 110.090 115.876 128.565
84 100.980 106.395 111.242 117.057 129.804
85 102.079 107.522 112.393 118.236 131.041
86 103.177 108.648 113.544 119.414 132.277
87 104.275 109.773 114.693 120.591 133.512
88 105.372 110.898 115.841 121.767 134.746
89 106.469 112.022 116.989 122.942 135.978
90 107.565 113.145 118.136 124.116 137.208
91 108.661 114.268 119.282 125.289 138.438
92 109.756 115.390 120.427 126.462 139.666
93 110.850 116.511 121.571 127.633 140.893
94 111.944 117.632 122.715 128.803 142.119
95 113.038 118.752 123.858 129.973 143.344
96 114.131 119.871 125.000 131.141 144.567
97 115.223 120.990 126.141 132.309 145.789
98 116.315 122.108 127.282 133.476 147.010
99 117.407 123.225 128.422 134.642 148.230
100 118.498 124.342 129.561 135.807 149.449
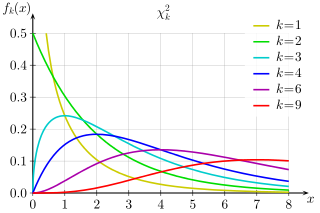
PDFs of chi-squared functions for first few values of k:
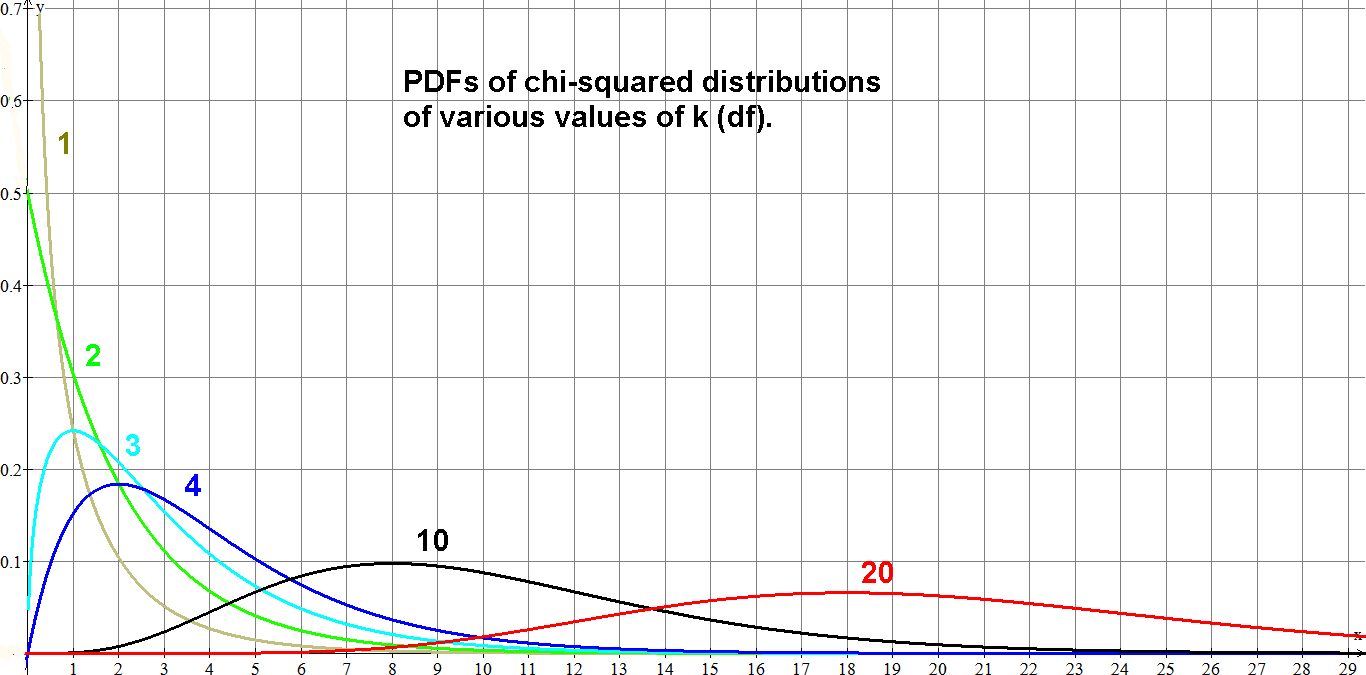
PDFs of chi-squared functions for various values of k:
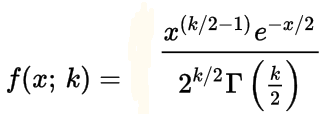 Γ gamma function
Γ gamma function
| k
| Γ(k/2)
| =/≈
|
| 1
| Γ(1/2)
| 1.7724
|
| 2
| Γ(1)
| 1
|
| 3
| Γ(3/2)
| .8862
|
| 4
| Γ(2)=1!
| 1
|
| 5
| Γ(5/2)
| 1.3293
|
| 6
| Γ(3)=2!
| 2
|
| 7
| Γ(7/2)
| 3.3233
|
| 8
| Γ(4)=3!
| 6
|
| 9
| Γ(9/2)
|
|
| 10
| Γ(5)=4!
| 24
|
| 20
| Γ(10)9!
| 362880
|
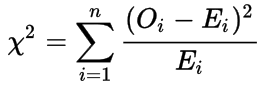



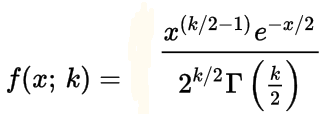 Γ gamma function
Γ gamma function