Confidence intervals

One Sample Interval for the Mean (t-Interval)

Confidence interval for a population mean μ: if do not know σ (this is usually the case).
t-test, t-procedure
Assumes population is Normal or sample size n>30.

sample size n:
sample mean x̄:
sample standard deviation s:

Margin of error:           tc = tα/2    α=1-CL    tc depends on n and CL.

Standard error of the mean (SEM)= s/√n:     df:


There is a CL% chance that   x̄±E   [x̄-E,x̄+E]   contains the true mean μ.
MSL: CL% confident that the limits ... actually do contain the value of the population mean μ. 

Try: 
37 100 15  At 95% CL E is ~5    At 99% CL E is ~6.7

100 100 10  vs. 1000 100 10   effect of sample size n
100 0 1  vs 1000 0 1 
 
100 0 1  vs 100 0 2   effect of sample standard deviation s

If know σ, use Z-test: Zc(σ/√n)
where Zc= 1.645 for 90% CL, 1.96 for 95% CL, 2.326 for 98% CL, 2.576 for 99% CL.

Minimum sample size n for given (estimated) σ, E, and C.L.=1-α


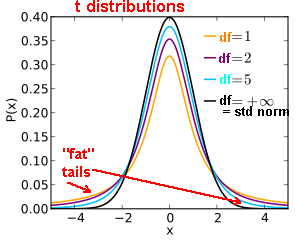
Fatter tails than the standard normal distribution because small samples have greater variability.
NB. There are no other t-distributions.

t distribution: ν=degrees of freedom
mean=0
σ=√(ν/(ν-2)) ν>2
skew= 0 ν>4, undefined 1,2,3
kurtosis= 6/(ν-4) ν>4, ∞ 3,4, undefined 1,2

df SD=√(df/(df-2)), df>2
1 undefined
2 ∞
3 √3≈1.732
4 √2≈1.414
5 √5/√3≈1.29
9 3/√7≈1.134

Standard error of the mean (SEM) for various s and n
s n
10 30 100 300 1000
1 .3162 .1826 .1 .0577 .0316
10 3.162 1.826 1 .5774 .3162
100 31.62 18.26 10 5.774 3.162