A positive number has two square roots. E.g. 9 has 3 and -3 as its two square roots: 32=9 and (-3)2=9
(0 has only one square root, itself, there being no -0.)
Radical symbol/sign: √ means principal (positive) square root of the radicand: √9
Square rooting as a unary operation: "take" the square root, by convention means the positive square root: √9 = 3 For the negative square root, include the negative sign: -√9 = -3
Negative numbers do not have a square root (in the Real number system).
Square root of a negative number is an error: √-25 calculator explodes. Is a complex number involving i which is √-1. √-25= 5i
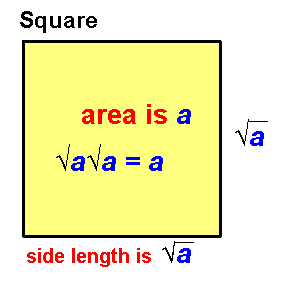
Geometrically, the square root of the area of a square is the side length of the square.
Square root sometimes denoted: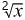 
A fractional exponent is defined as: 
Thus √x = 
The extending "bar" is called a vinculum.
√2ax+b
(In text situations, like here, it might not be perfect.)
√a√a = a
√9√9 = 3·3 = 9
√a2 = |a|
√92 = √81 = 9 √(-9)2 = √81 = |-9|
√9 is a number, 3. So √9 = 3
When solving a quadratic equation and it's been reduced to the form √x2=c,
then x has two solutions, ±√c
Square root of a perfect square, a positive integer/whole number that is the
square of a whole number, 0,1,4,9,16,25,36,49,64,81,11,121,144,169,...
is an integer. E.g. √4=2, √25=5, √144=12, √1=1
Square root of other integers/whole numbers is an irrational number.
E.g. √2≈1.414214 √3≈1.732051
√5≈2.236068 √40≈6.324555
(Same thing applies to higher roots:
--cube root of a perfect cube [0,1,8,27,64,125,...] is an integer, cube root of non-perfect cubes is irrational,
--fourth root of a perfect fourth power "quarts" [0,1,16,81,256,625,...] is an integer, fourth root of non-perfect "quarts" is irrational,
etc.)
Some fractions are perfect squares: 1/4, 1/9,..., 4/9, 9/4, 16/49, ... Their square root
is rational: √(4/9)=2/3
Square root of a non-perfect integer might be simplifiable (i.e. make the radicand
as small as possible, i.e. no factors that are perfect squares) using this fact:
Product rule for square roots:
√ab = √a√b Useful if factors a or b is a perfect square.
√40 = √(4·10) = √4√10 = 2√10
≈2·3.162278 ≈6.324555
√6 = √2√3 but one √ is usually simpler.
√x+√x = 2√x ≠ √(2x) = √2√x
2√5 ≠ √10 = √2√5
Roots of from 0 to 20
100x100 multiplication table, takes root
1/√a = √(1/a)
There is no "sum rule": √(a+b) ≠ √a+√b
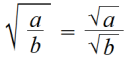
Square root of (non-integer) positive real numbers may or may not be rational:
√10.24=3.2 √10.23≈3.1984371
Is rational if the significant digits multiplied by a power of 100 is a perfect square.
e.g. 10.24*100 = 1024=322, so √10.24, √102400, √.1024, etc are rational.
but √1.204, √0.01024, √102.4, √10240, etc are not.
Square root function:
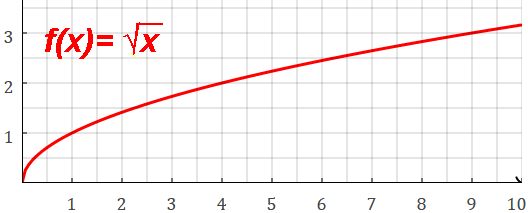
It's the positive, upper half of the parabola x=y2
It's a slow-growing function:
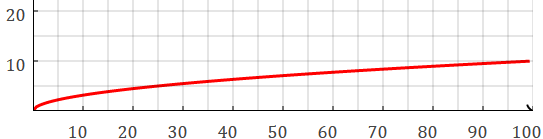
NB. square root of a number less than 1 is bigger than the number:
Derivative of √x function is 1/√x.
Integral of √x function is ⅔x3/2
√2 ≈ 1.414213562373 ≈ 1.414 (14 14, year 1414 start of the Council of Constance that resolved the multiple anti-popes problem, condemned and burned Jan Hus for heresy, and papal secretary Poggio Bracciolini discovered and had copied the manuscript of Lucretius's De rerum natura
√3 ≈ 1.732050807568 ≈ 1.732 (1732 George Washington's birthday)
The reciprocal of √2 equals one half of √2: 1/√2 = √2/2 ≈ 0.707
The reciprocal of √3 equals one third of √3: 1/√3 = √3/3 ≈ 0.577
The reciprocal of √n equals one Nth of √n: 1/√n = √n/n
a+b conjugate is a-b
(a+√b)(a-√b) = a2-b
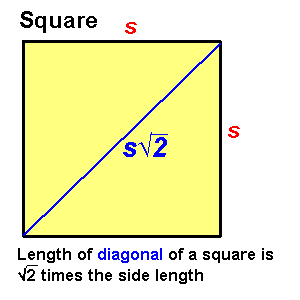
Length of hypotenuse of a right triangle is specified by the Pythagorean theorem:
Height of equilateral triangle of side s is s√3 /2
is the long leg of a 30-60-90 triangle.
Distance d to horizon given height h miles above ground/sea level:
Distance in km to horizon given one's height h above sea level in meters: 3.57√h
Distance in km to thing at height h2 above sea level given one's height h1 above sea level in meters: 3.57√h1 + 3.57√h2
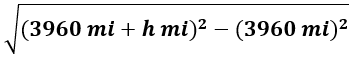
Heron's formula for the area of a triangle, given the lengths of its sides a, b, c:
semiperimeter s = (a+b+c)/2 i.e. half the perimeter
A = √(s(s-a)(s-b)(s-c))
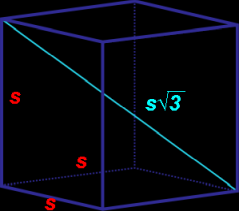
Length of internal diagonal of a cube is √3 times the side length:
Length of diagonal of rectangular box (parallelpiped) of side lengths x, y, and z is √(x2+y2+z2)
Distance between two points formula:
Distance between points (a,b) and (b,a) is √2|a-b|.
Line between them is y=-x+(a+b)
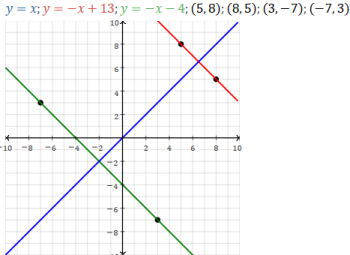
Distance between points (a,a) and (-a,-a) is 2a√2
Distance between points (a,b) and (-a,-b) is 2√(a2+b2)
Quadratic formula to solve quadratic equations:
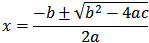
Standard normal distribution:
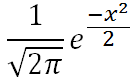Slope at inflection point: m=±1/√(2πe)
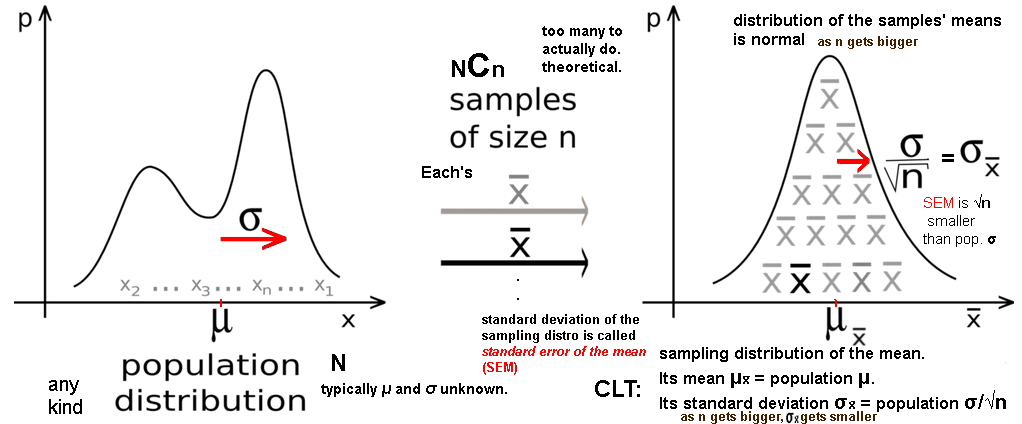
Central Limit Theorem of statistics:
the standard deviation of the means of all samples of a given size n
from any population will be 1/√n of the standard deviation of the population.
Standard deviation:
Root mean square (RMS) of
a set of values is the square root of the mean of the squares of the data:
Average (or expected) difference between two data values randomly chosen
from a normal distribution is 2σ/√π ≈1.128σ
Mean absolute deviation of a normal distribution: MAD = σ√(2/π) ≈.7979σ
Uniform distribution: σ = (end-start)/√12 ≈(end-start)/3.464
~57.75% of data within 1 σ of mean
Binomial distribution: σ = √(np(1-p))
Poisson distribution: σ = √λ
Χ2 Chi-squared distribution: σ = √(2k)
All of the data in a uniform distribution is within √3 standard deviations of the mean.
A-series of paper sizes: aspect ratios (i.e. ratio of width to length) is 1:√2. Enables folding in half or doubling to be in same ratio.
Golden Ratio
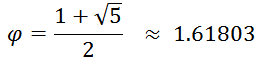
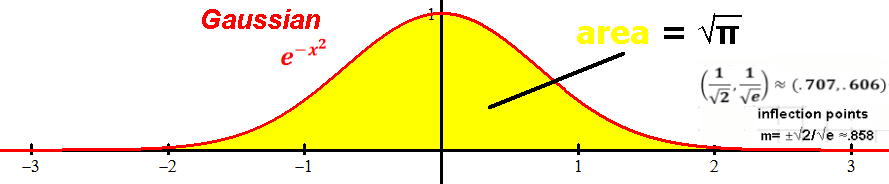
Simplest Gaussian function: e-x2 = 1/ex2
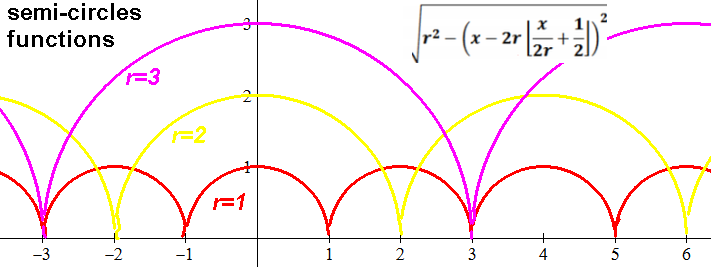
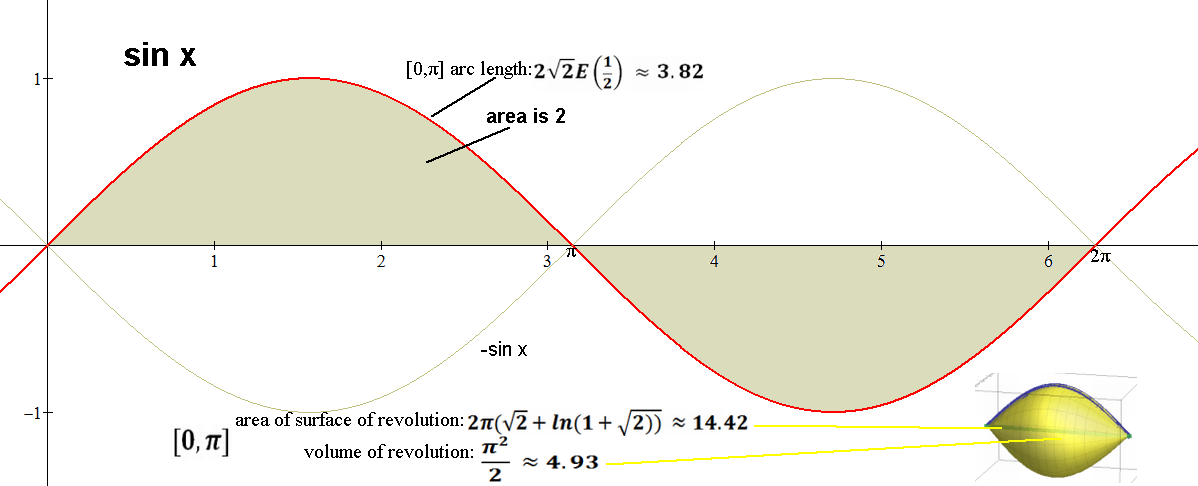
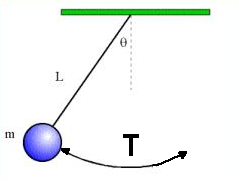
Period (time for complete roundtrip swing back and forth) of a pendulum:
T = 2π√(L/g) L=length of arm g=9.8(metric)=32(US)
Time t in seconds to fall h feet near the surface of the Earth is √(h/16).
Time t in seconds to fall h meters near the surface of the Earth is √(h/5).
Terminal velocity of a falling object near Earth's surface=
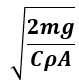
m=mass, g=gravity acceleration 9.81m/s2, C=drag coefficient 0.5≤C≤1.0,
ρ=air density 1.2 kg/m3, A=cross-section area
Velocity V, in feet per second, of water discharged from a nozzle of pressure P in psi: V = 12.14√P
The current I, in amperes, in a circuit is √(P/R), where P is power in watts and R
is resistance in ohms.
The voltage V, in volts, in a circuit is √(Pr), where P is power in watts and r
is resistance in ohms.
BSA (body surface area) m2 ≈ √(WH) / 60 [kg,cm] ≈ √(1.15wh) / 60 [lbs,in]
BRI (body roundness index) = 364.2 - 365.5√(1-(waist/(π*height))^2)
3-6 is good
Trigonometric functions' values at 30°, 45°, 60°:
Click for larger image.
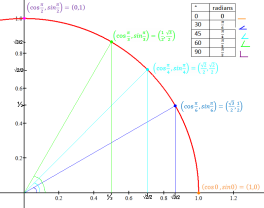
Click for larger image.