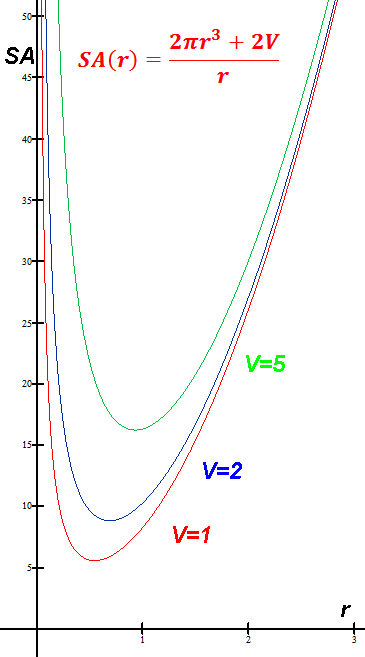
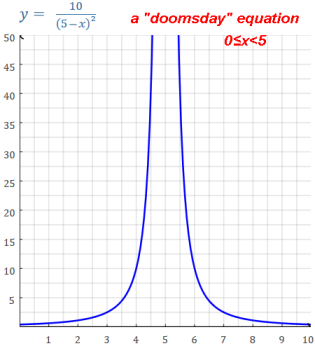
Examples:
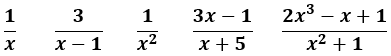
A polynomial over a polynomial, denominator can't be zero. cf. rational number: integer over integer, no zero denominator.
Interesting stuff: might have:
domain restrictions,
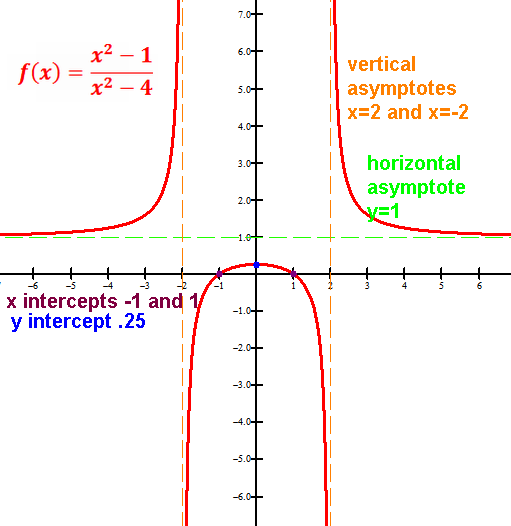
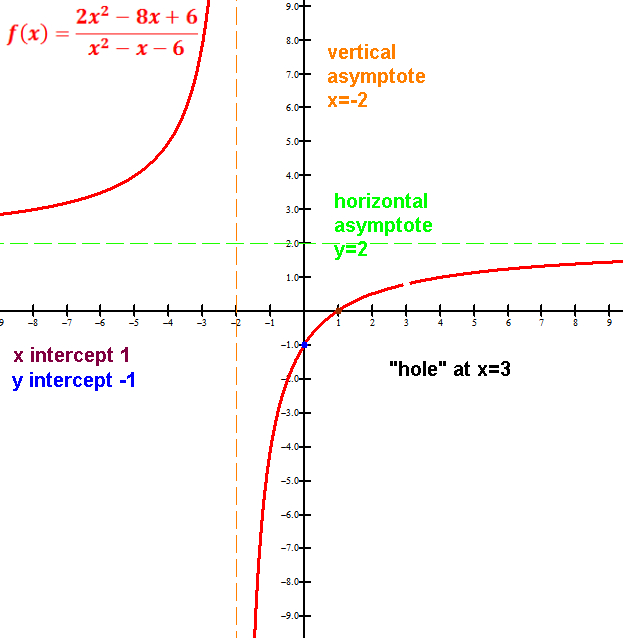
x intercept(s),
y intercept,
absolute or local extrema,
symmetry,
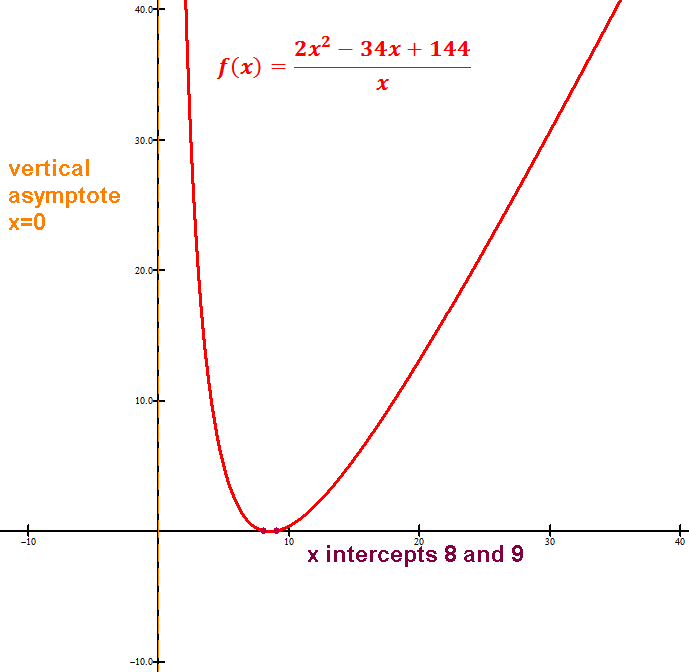
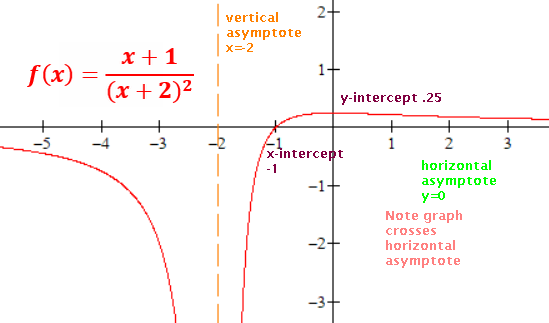
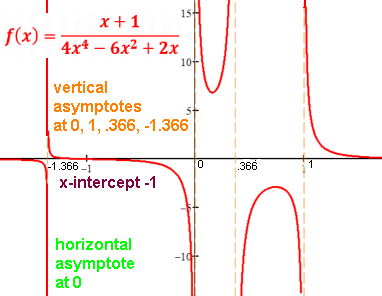
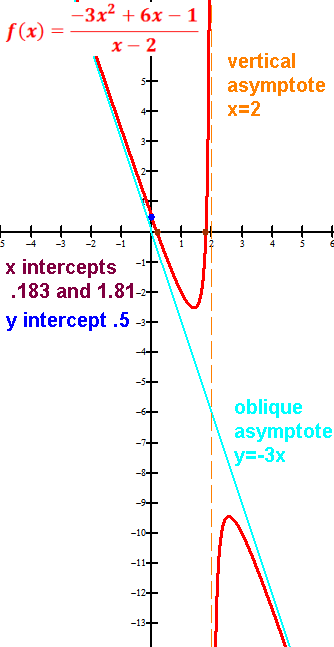
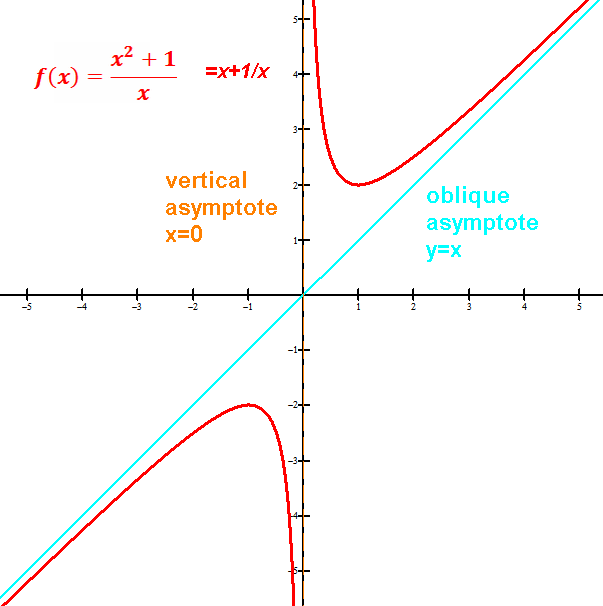
*vertical asymptote(s),
*a horizontal or oblique asymptote,
*"holes"
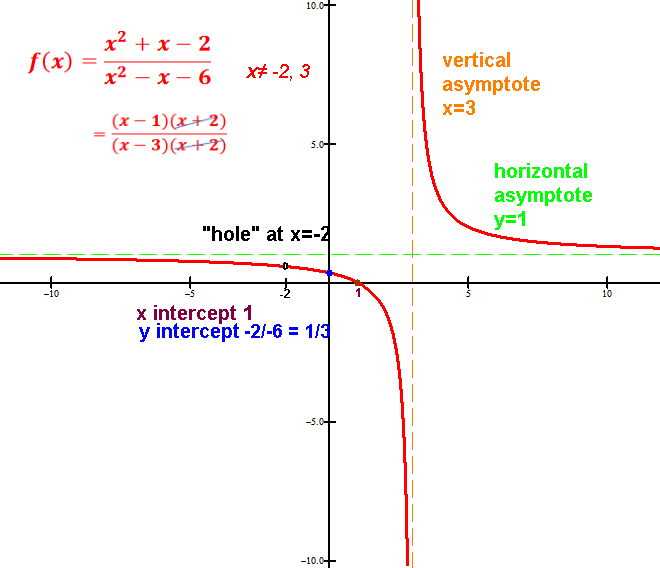
Domain of rational function is R minus the values that make q(x) denominator zero (each of these will be either a vertical asymptote or a hole).
The polynomials can simplify by cancelling common factors.
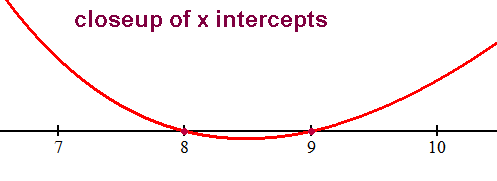
x-intercept(s), if any, are the zeros of the simplified numerator p(x), i.e. p(x)=0 Solve.
I.e. what value(s) make the numerator zero (and are in the domain).
The simplified numerator function is a polynomial of degree n → can be as many as n X-intercepts,
more precisely n or n-2 or ...or 1 or 0 of them.
y-intercept: set x to 0, if possible, i.e. 0 is in domain
(else there is no y-intercept).
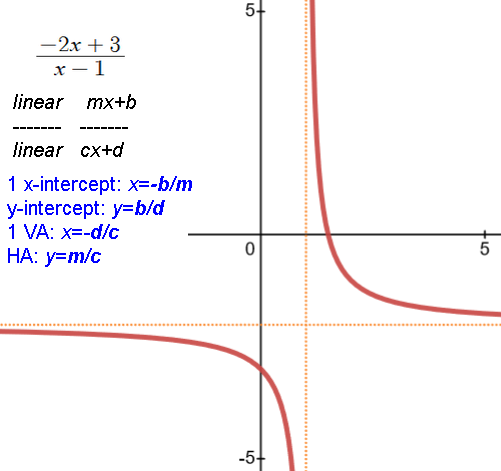
The ratio of the two constant terms of p and q.
If numerator has no constant and denominator does, y-intercept is 0
If denominator does not have a constant, there's no y-intercept.
Asymptote: a line that a curve gets closer and closer to.
Vertical asymptote(s), if any, at x's that make the simplified denominator 0,
(i.e. after all cancellations between numerator and denominator,
i.e. the rational function is in lowest terms.)
n-degree simplified denominator → ≤n vertical asymptotes.
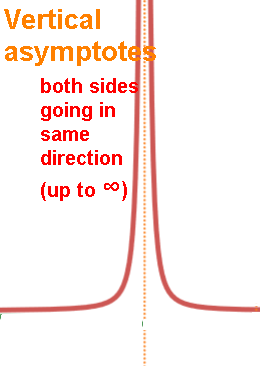
Both "sides" at the VA go in same "direction" (i.e. both up or both down) or in opposite "directions"
(i.e. one up, the other down).
A discontinuity.
Graph them as dotted orange lines (unless is an axis).

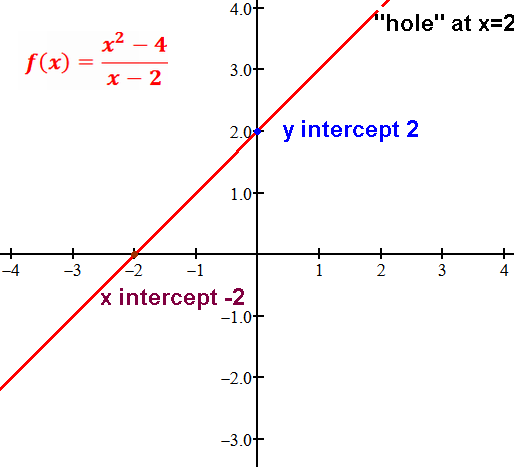
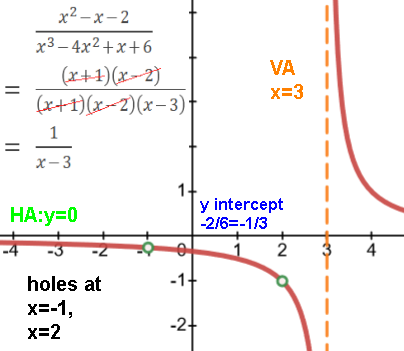
An x value that makes the original unsimplified denominator 0 but not the simplified one is a hole.
The x is not in the domain, so that (x,f(x)) point is a single-point hole.
A discontinuity.
If the denominator q, or D, is a factor of p, or N,
this can simplify to a polynomial function. Example:
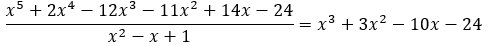
But any x values that make the q(x) zero are "holes".
"End behavior":
What happens as x approaches ±∞.
Horizontal asymptote:
Dominant/leading terms of numerator and denominator: 3 cases
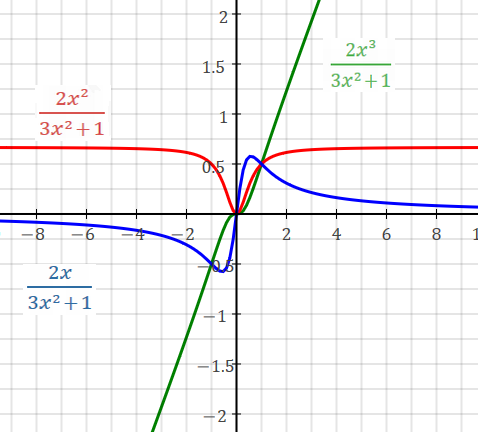
1. If degrees of N and D are the same:
axn/bxn --> Horizontal asymptote at y = a/b
E.g.: 2x/3x 2/3 5x2/x2 5 3x3/2x3 3/2 ...
xn/xn --> y=1 Special case when a=b=1.
E.g.: x/x x2/x2 x3/x3 ...
2. If degree of N is less than degree of D: (a proper rational function)
xi/xj i<j --> Horizontal asymptote at y = 0
E.g.: x/x2 x/x3 ... x2/x3 x2/x4 x3/x4 ...
If have a H.A. (cases 1 or 2), both "ends" approach the same H.A.
3. If degree of N is greater than degree of D:
xi/xj i>j --> no horizontal asymptote.
Ends go to infinities.
E.g.: x2/x x3/x ... x3/x2 x4/x2 x4/x3 ...
Except see below for oblique asymptote if degree of N is one more than degree of D.
If a rational function has a H.A., both "ends" approach the same H.A.

Graph can cross horizontal or oblique asymptote but not vertical asymptotes.
Find any x such that R(x)=horizontal asymptote
Symmetry.
Some are odd, some even, some neither even nor odd but have rotational symmetry around some point, others
don't.
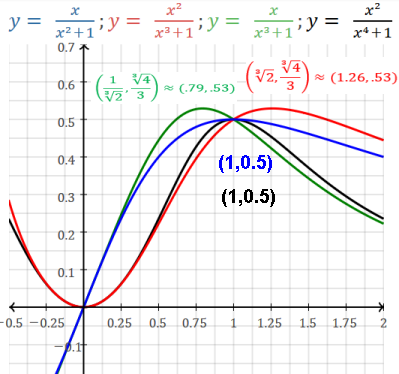
Examples:
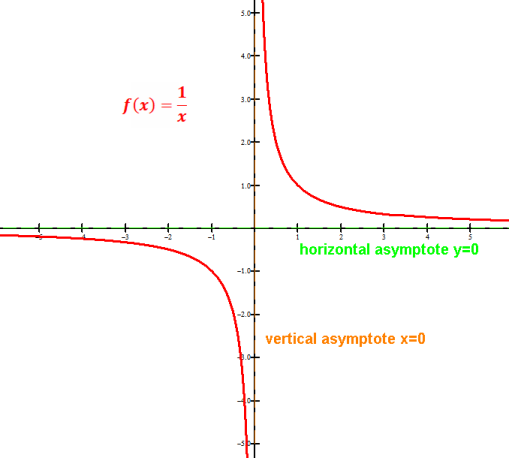
1/x no intercepts, 0∉domain→VA at x=0, HA y=0, odd, decreasing
1/(x-1) no x-intercepts, y-intercept at -1, 1∉domain→VA at x=1, HA y=0
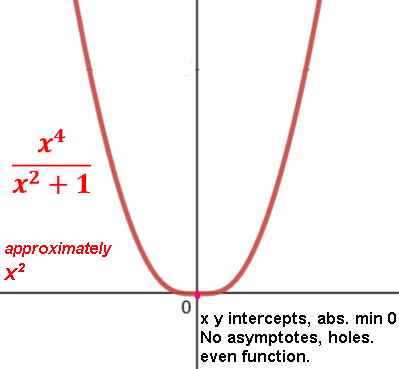
(x4+1)/(x2+1) no x-intercepts, y-intercept at 1, no asymptotes, even
1/x2 no intercepts, 0∉domain→VA at x=0, HA y=0, even
1/(x2-x) no intercepts, 0,1∉domain→ VAs at x=0 and x=1, HA y=0
1/(x3-x2-x) no intercepts, 3 VA at x=0,φ,1-φ, HA y=0:
(x2+5)/(x2+1) no x-intercepts, y-intercept at 5, HA y=1
(x5+1)/(x2+1) x-intercept at -1, y-intercept at 1
(x4-5x2+4)/(x2-3) 4 x-intercepts at ±1 and ±2,
y-intercept at -4/3, ±√3∉domain→VAs at x=±√3, no HA, even