Arithmetic operations on real numbers.

Operation Symbols used Result's name Notes
addition a + b sum "a plus b"
a,b terms added or subtracted
commutative: a+b=b+a
associative: (a+b)+c=a+(b+c)
0 is the identity: a+0=a
a, -a inverses: a+-a=0   †
subtraction a - b difference "a minus b" "difference of a and b"
Same as adding the additive inverse: a+-b
Not commutative: a-b≠b-a
Not associative: (a-b)-c≠a-(b-c)
Addition and subtraction are inverse operations. a+3=b, b-3=a
multiplication a × b
a · b
ab (juxtaposition) 5a 5x (5)(6)

a * b 		product "a times b"
shortcut repeated addition: add a to itself b times, or b to itself a times
a,b factors
commutative: ab=ba
associative: (ab)c=a(bc)
1 is identity: a·1=a
a, 1/a inverses: a·1/a=1   †
distributes over addition: a(b+c)=ab+ac
   
If ab=0 then a=0 or b=0 (or both)
a·0=0
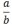
division a ÷ b


a / b 		quotient "a divided by b" "quotient of a and b"
shortcut repeated subtraction. [Or: a/b=a*(1/b)]
Not commutative: a/b≠b/a      
Not associative: (a/b)/c≠a/(b/c)
1/a is the reciprocal of a , its multiplicative inverse
Multiplication and division are inverse operations. ab=c, c/b=a
exponentiation bp (superscript)

b^p 		power "b [raised] to the pth power" "b to the pth"
b is base, p is exponent or power.
shortcut repeated multiplication (of a number times itself multiple times) a4=a*a*a*a
b2 "squared"    b3 "cubed"     b0=1     b1=b
Laws:
   xmxn=xm+n   Product rule
   (xy)m=xmym
   (xm)n=xmn   Power rule
   xm/xn=xm-n   Quotient rule
   (x/y)m=xm/ym
   x-n=1/xn   Negative exponent rule
   x-1=1/x
NB. x+x=2x    x·x=x2
square root √a   (radical)

sqrt(a) 		root radicand a≥0       √a=a1/2
positive (principal) root
√a2=|a|
√a√a=a
√of non-perfect square integer is irrational
√(ab)=√a√b    √(a/b)=√a/√b
Squaring and square root are inverse operations. a2=b, √b=a
negation -a flip across 0 on number line
If a>0, then -a<0   
If a<0, then -a>0    --2=2
Same as *-1
|a| = |-a|
absolute value |a| the positive of a
If a>0, then |a|=a (already is positive).   |2|=2
If a<0, then |a|=-a (makes the negative positive).   |-2|=2
|a| = distance of a from 0
|a-b| = |b-a| distance between a and b
reciprocal 1/a reciprocal of reciprocal of a is a: 1/(1/a)=a
reciprocal of a/b is b/a
Division can be defined: a/b = a*(1/b)
Reciprocal is its own inverse operation.
† number ⊛ inverse = identity

Symbol is a shortcut for the word. Word is a shortcut for the concept.

P E M
D		A
S
is an agreement on the order of operations so as to not have to use parentheses for every operation:
5+24·3-6/4+1    ≡    (((5+((24)·3))-(6/4))+1)

Addition is the fundamental operation, the others (-,*,/,^) can be defined in terms of it. Viz. subtraction is addition of additive inverse, multiplication is repeated addition, division is repeated subtraction, exponentiation is repeated multiplication.

Opposites/inverses: addition/subtraction, multiplication/division, squaring/square-rooting

Z not closed under division. Q not closed under square root.
Possible: I*I=Q