Newton's law of cooling / warming

T(t)=Ta+(T0-Ta)e-kt

Initial temperature of substance (T0):
Ambient temperature (Ta):
Experimentally measured temperature: at time t: determines k     OR     k:

Time to reach temperature of°     OR     Temperature reached after time oftime units.
"half-life":(time for half of the termperature gap)

Newton's law of cooling.
Cooling (i.e. loss of energy as heat) of something is proportional to the difference between its temperature and the ambient temperature (i.e. the temperature of its surroundings).

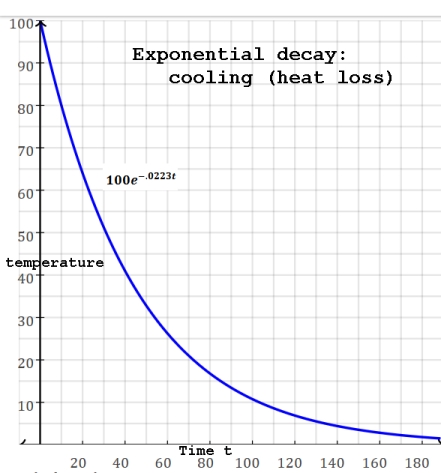
Say a kettle of 100° boiling water is taken off the stove and put into a very large refrigerator/freezer that is at 0°. (and ocasionally stirred).
After 10 minutes the temperature of the water is measured to be 80°.
Ambient temperature: Ta=0     Temperature at time 0: T0: T(0)=100     
Temperature at time m=10: Tm=T(10)=80
Temperature at time t: T(t)=Ta+(T0-Ta)e-tk
Temperature at time 10: T(10)=Ta+(T0-Ta)e-10k     Solving for k: 80=0+(100-0)e-10k     k=.0223      T(t)=100e-.0223t      half-life: ln 2 = kt      t=31.08

Time of the excess temperature to halve from any value is always the same. (Excess temperature is T0-Ta)
The heat (energy) has a "half-life".

Another example: something hot at 80° placed into 20°. After 15 minutes it is 65°.
T(15)=Ta+(T0-Ta)e-15k      Solving for k: 65=20+(80-20)e-15k      k=.0192      T(t)=20+60e-.0192t      half-life: ln 2 = kt     t=36.1