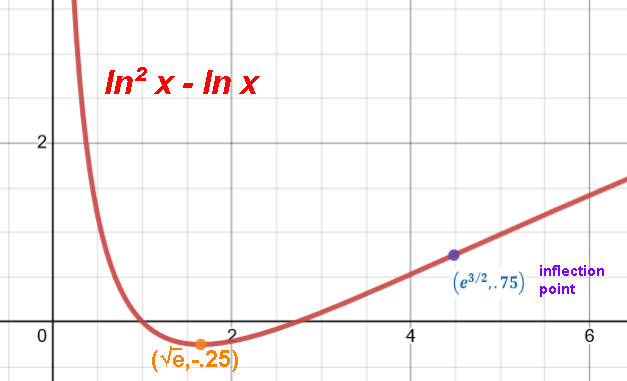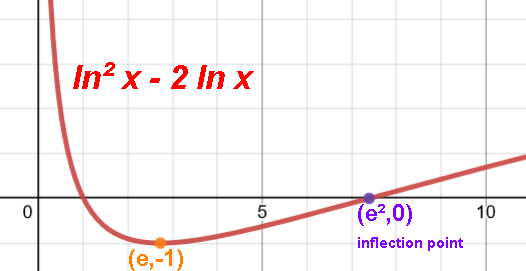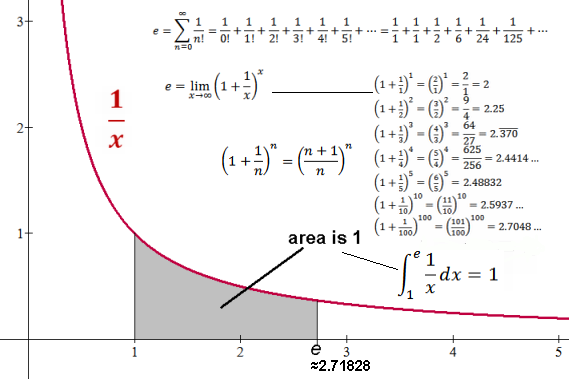
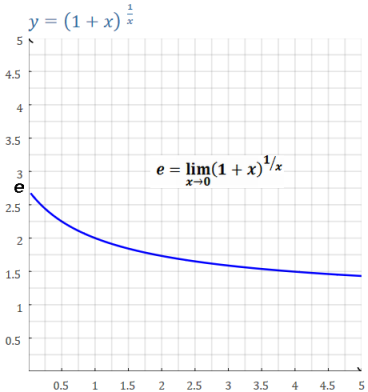
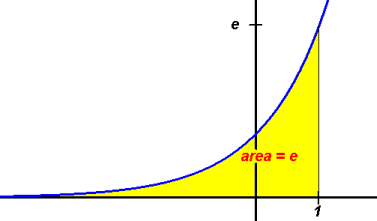
e geometry: the area under the simplest hyperbola 1/x from 1 to e is 1.
eefing amazing:

e geometry: the area under the simplest hyperbola 1/x from 1 to e is 1.
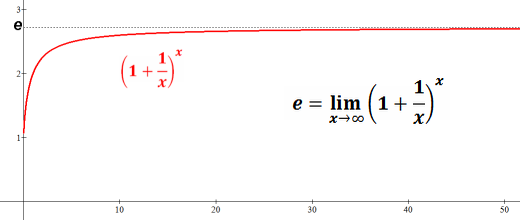
Can get to e in a limiting process:


Some relations with π, i, trig functions:
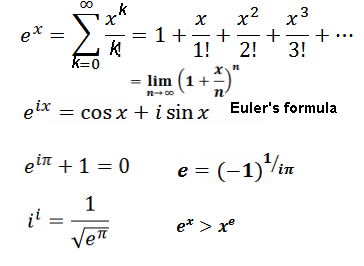
Money with e:
future value FV (accumulated value) of continuosly compounded interest r of principal P in t years:
FV = Pert
(continuous growth. inflation etc.)
"e is an interesting number" "It sure is pertty"
ex: the exponential function.
| e1 | 2.71828 | e-1 | = 1/e = .36787 | |
|---|---|---|---|---|
| e2 | 7.38905 | e-2 | .13533 | |
| e3 | 20.08553 | e-3 | .049787 | |
| e4 | 54.5981 | e-4 | .018315 | |
| e5 | 148.4132 | e-5 | .006779 | |
| e6 | 403.4287 | e-6 | .0024787 |

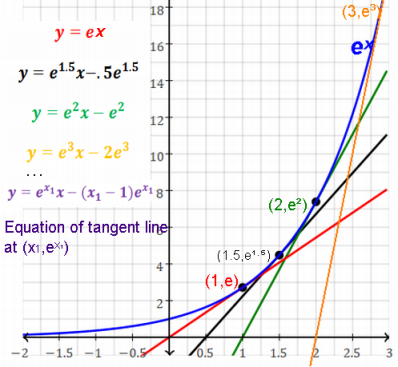
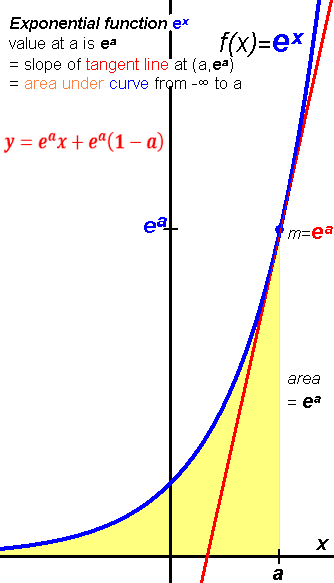
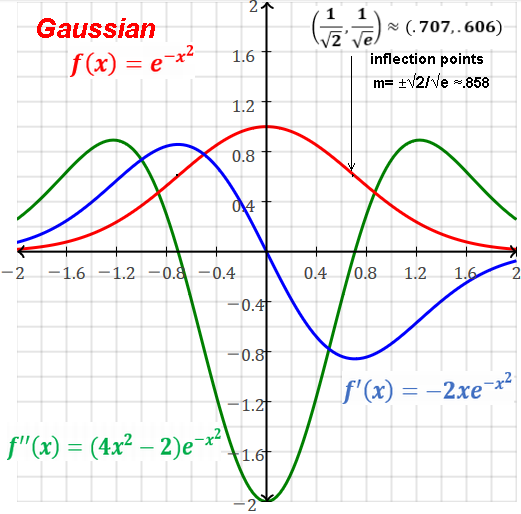
Exponential function is the only function whose derivative is itself,
i.e. (ex)' = ex
i.e. slope is itself. "Most important property"
NB. derivative of general exponential function bx is bx ln b
So the slope of the tangent line at any point on ex curve is ex.
i.e. the rate of change at x is equal to the y (height).
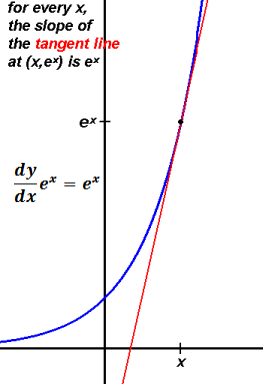
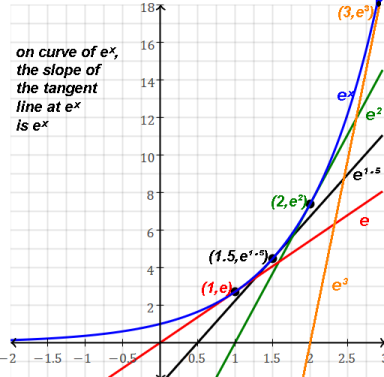

Here are some example tangent lines at various points on ex.

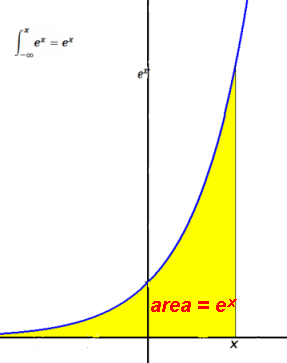
Exponential function is the only function whose integral is itself.
So the area under the curve of ex from -∞ to x is ex.

In summary:
Exercise:
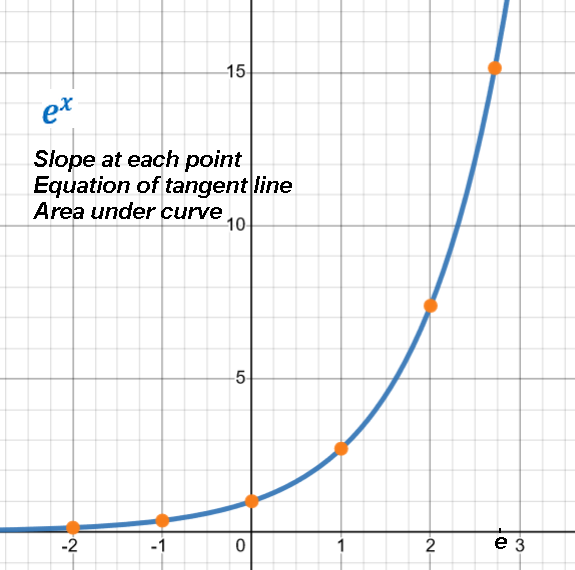
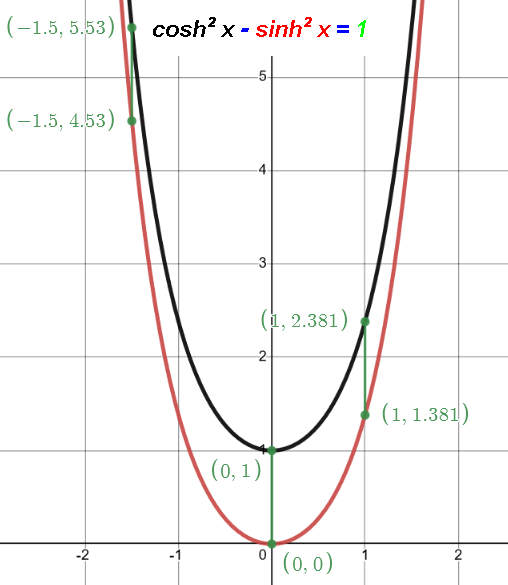
ex and its reciprocal 1/ex = e-x.
Symmetric about Y axis.


Average of ex and e-x is the
hyperbolic cosine function, cosh.
Half the difference of ex and e-x is the
hyperbolic sine function, sinh.
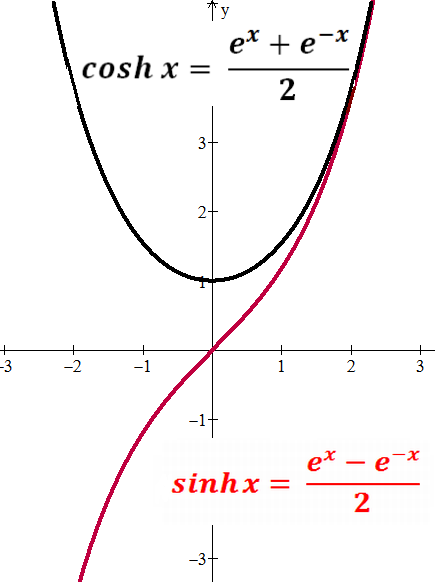

cosh'=sinh and sinh'=cosh
The only pairs of functions that are each other's derivative all have this form:
f(x)=aex+be-x and g(x)=aex-be-x
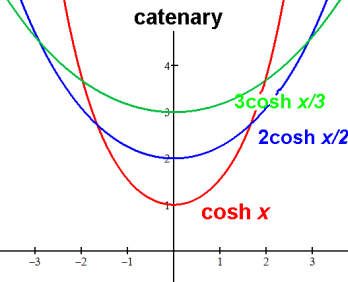
Hanging/sagging/drooping chain/rope/cable is a catenary curve: a cosh(x/a)
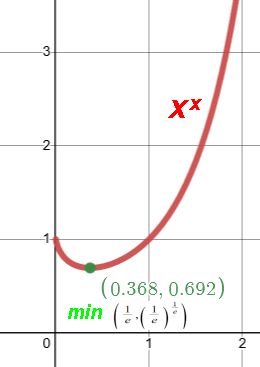
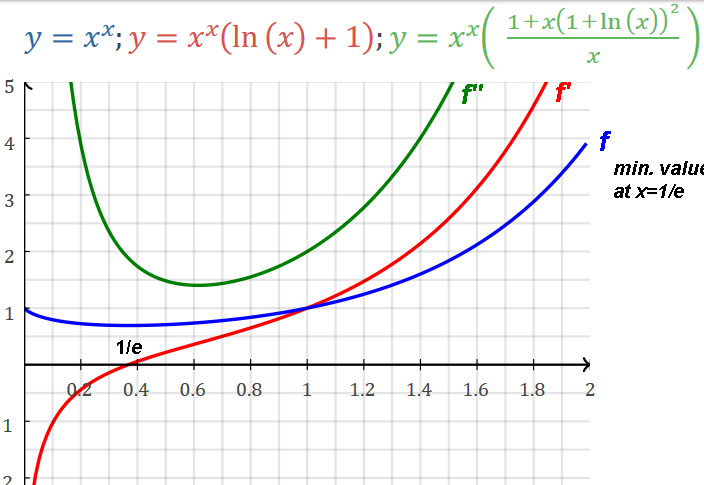
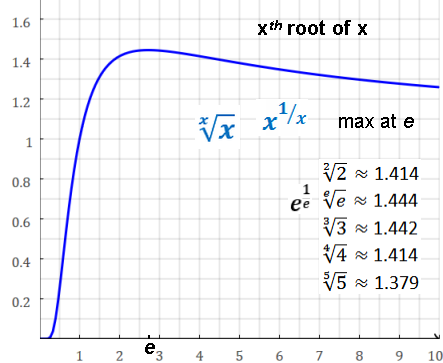
Steiner's problem: where's the max value of x1/x? i.e. xth root of x

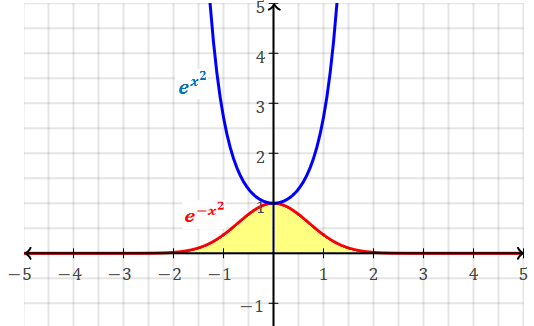
ex2 and e-x2.
Not exponential but use e.
e-x2 is the [simplest] Gaussian function.
Its infinite integral (i.e. area under its curve) is √π≈1.772.
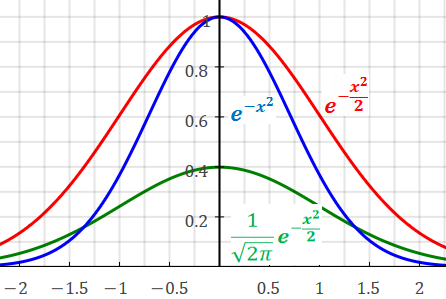
The standard normal distribution:
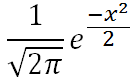
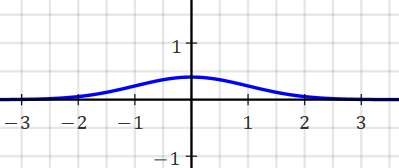
Gaussian/normal distribution function:
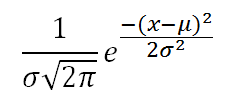
Poisson distribution.
the probability that k events will happen in an interval
given that the average/expected number of random independent events
in an interval is λ is:
(λke-λ) / k!
//return a Poisson-distributed random number
//given lambda=expected/average independent #events in an interval
function poisson(lambda) {
var k=0, p=1, L = Math.exp(-lambda);
do {
k++;
p *= Math.random();
} while (p > L);
return k-1;
}
Derangements
A derangement is a permuatation that is a complete rearrangement,
i.e. all items move.
Example: bca and cab are the two derangements of abc.
Example: badc bcda bdac cadb cdab cdba dabc dcab dcba are the nine derangements of abcd.
Probability of a permutation being a derangement
is 1/e (in the limit as n→∞)
≈ 0.367879441
≈ 36.78% of permutations are derangements
#permutations = n! #derangements !n = floor(n!/e + 1/2)
n:!n 3:2 4:9 5:44 6:265 7:1854 8:14833 9:133496 ...
n!/!n = e
Factorials

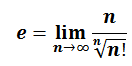
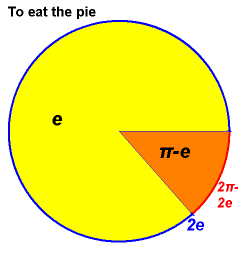
Roll an n-sided die n times. Probability never is a particular side (e.g. a 1) is 1/e.
If have N equally likely outcomes. Do N experiments. Probability that a certain outcome
never happens is 1/e.
Gambling game: N slots, one the winner. N tries(plays). Chance of losing all (ie. never winning) is 1/e.
demo
The average number of random real numbers between 0 and 1 needed to sum
to more than 1 is e.
I.e. need an average of e numbers uniformly distributed in [0,1] to sum >1.

demo
A stick of length L broken into n equal-length pieces. Multiply the lengths of all the pieces.
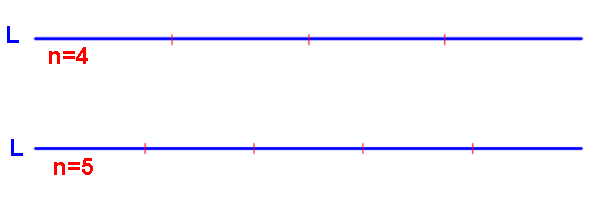
What value of n maximizes the product? ⌊L/e⌋ or ⌊L/e⌋+1
demo
The probability of selecting/picking/encountering the best/highest of randomly
presented/ordered candidates/items/numbers
as the proportion x of them presented/encountered.
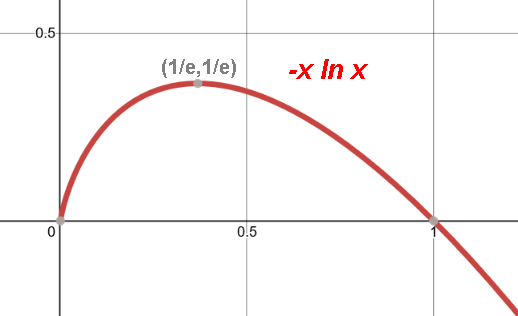
Secretary problem. Have N rankable candidates, want the optimal. See them sequentially in random order,
once seen can not be considered again, choosing one stops the process. .
Algorithm: see 1/e of them remembering the rank of the best of them, then choose next that is better.
Has 1/e (37%) chance of choosing the best.
demo
Primes
The Prime Number Theorem: π(N), the number of primes up to N, is approximately N/ln N.
(which equals eN/N)
| N | ln N | N/ln N | π(N) | %primes |
|---|---|---|---|---|
| 106 | 13.81 | 72,382 | 78,498 | 7.8498 |
| 109 | 20.72 | 48,254,942 | 50,847,534 | 5.0847534 |
| 1012 | 27.63 | 36,191,206,825 | 37,607,912,018 | 3.7607912018 |
| 1015 | 34.54 | 28,952,965,460,216 | 29,844,570,422,669 | 2.9844570422669 |
Partitions
p(n) = #partitions of a positive integer n
(i.e. #ways that n can be written as a sum of positive integers)
p(4)=5 : 4, 3+1, 2+2, 2+1+1, 1+1+1+1
p(5)=7 : 5, 4+1, 3+2, 3+1+1, 2+2+1, 2+1+1+1, 1+1+1+1+1
Euler's constant
γ ≈ 0.57721. Difference between the sum of a harmonic series of n terms and
ln n approaches γ as n approaches ∞.

Alternating harmonic series
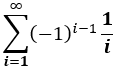 =
1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + 1/7...= ln 2 ≈.693147
=
1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + 1/7...= ln 2 ≈.693147
Google's IPO goal was to raise $2,718,281,828 (e billion dollars)
Entropy S = k ln W
The number of Ways the system can be.
"I think that I shall never see a number as lovely as e."
Logarithmic spirals.
x(t)=aebtcos(t)
y(t)=aebtsin(t)


"e must be dear to the Diety."