Calculate a Z-score.

z = (x-mean) / SD
Population Sample Sample mean
   z = (x - μ) / σ       z = (x - x̄) / s       z = (x̄ - μ) / (σ/√n)   

mean: μ or x̄:
SD: σ or s or σ/√n:
x:

CDF from Z score

z score:

Left: P(≤z) = CDF(z) =    % of data less than this Z score (= area under the standard normal curve from -∞ to this Z score)
Right:P(≥z)=1-CDF(z)==α    % of data greater than this Z score (= area under the standard normal curve from this Z score to ∞)
(calculate Z score from CDF or 1-CDF probability, and reset X)


Between: P(az≤Z≤bz)           az bz     
OR           P(ax≤X≤bx)          ax bx      (define μ and σ above)
=CDF(bz) - CDF(az)
=

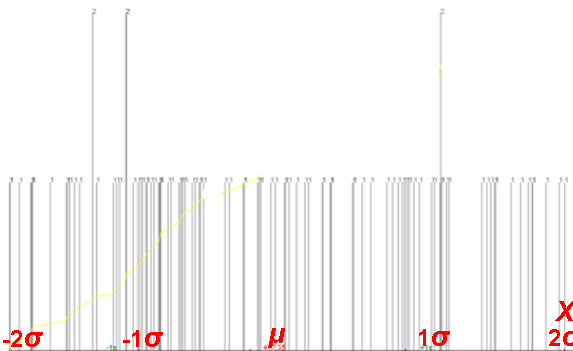
A data set:   its Z scores:


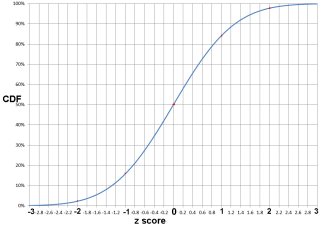
N = 100M
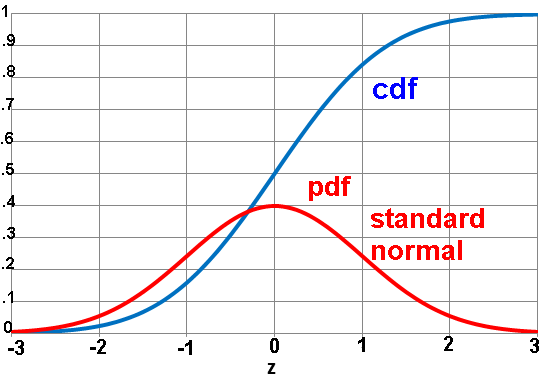
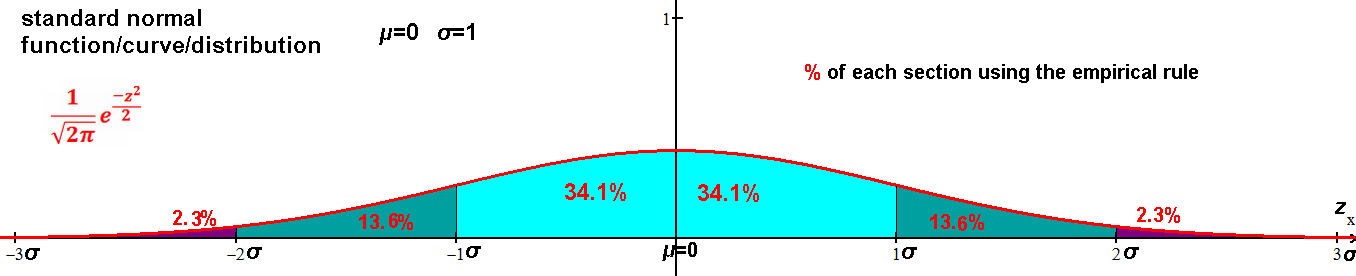
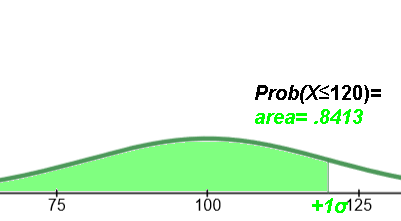
≤μ   .5 ≥μ   50% ½ 50M
≤μ+σ   .8413 ≥μ+σ   15.87% 1/6.3 15,870,000
≤μ+2σ   .9772 ≥μ+2σ   2.28% 1/44 2,280,000
≤μ+3σ   .9987 ≥μ+3σ   .13% 1/769 130,000

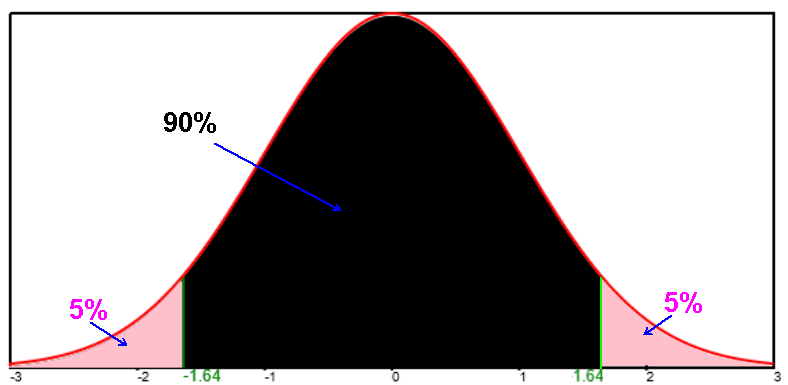
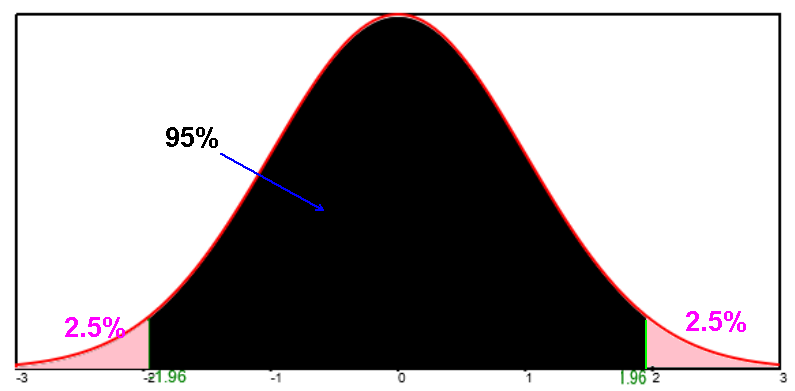
Critical values: zc= 1.645 for 90, 1.96 for 95%, 2.326 for 98%, 2.576 for 99%

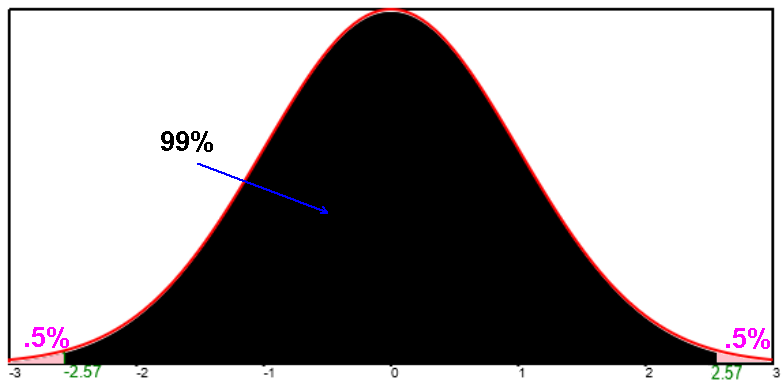
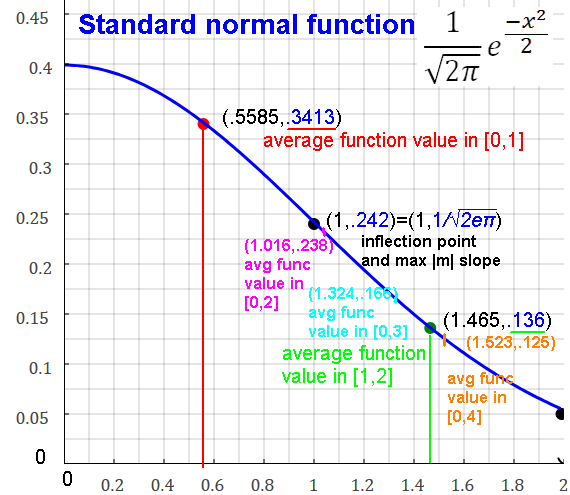
Quartiles and deciles of the standard normal distribution.

All normal curves: area under the curve equals 1.

The standard normal function/curve/distribution: mean μ=0. standard deviation σ=1.

Any Z score is the number of standard deviations from the mean 0 of this standard normal curve.

Function of x (or z):
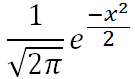  equivalently: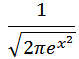 


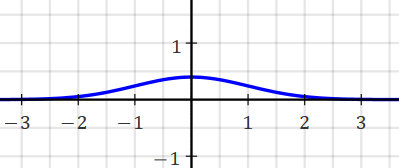
Mathpapa:
y=1/(sqrt(2*PI)) * e^(-x^2/2) 
Desmos:
y=1/(\sqrt{2\cdot\pi})\cdot e^{(-x^{2}/2)}

(vertical exaggerated to see the "bell"):

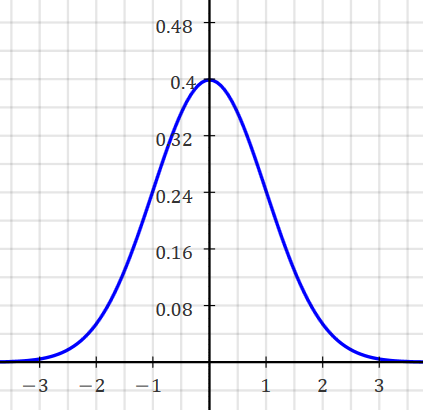
f(0)=1/√(2π) ≈.3989

MAD = √(2/π) ≈ .798
Average difference between two data values randomly chosen from the standard normal distribution is 2/√π ≈ 1.128 = MAD√2

σ=1/√2π=1/2.5066= .3989    → PDF(0)=1


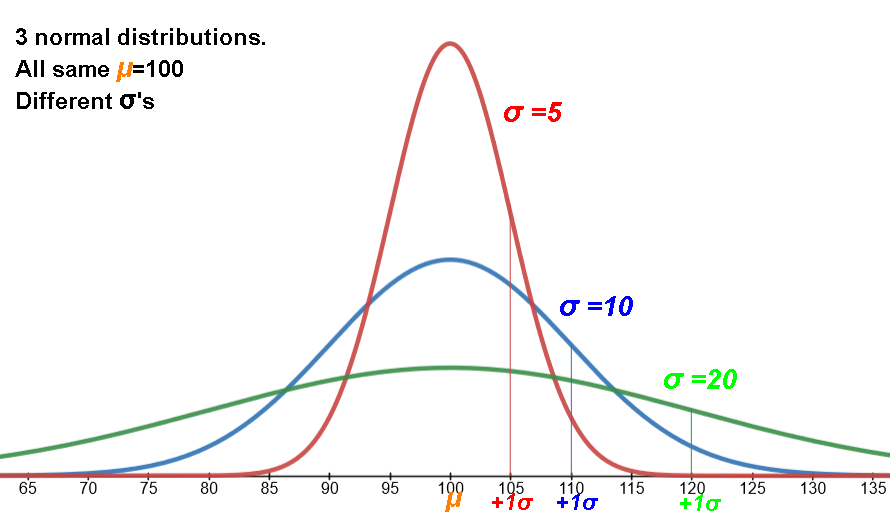
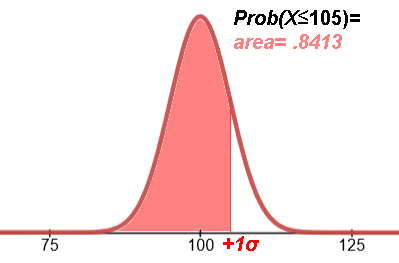
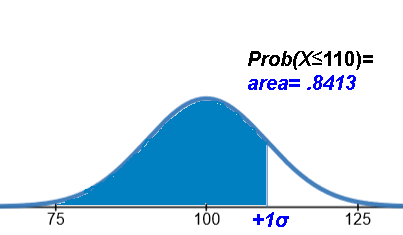
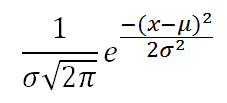example normal functions/curves/distributions

Function of x. μ and σ determine each particular curve.
equivalently: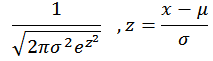

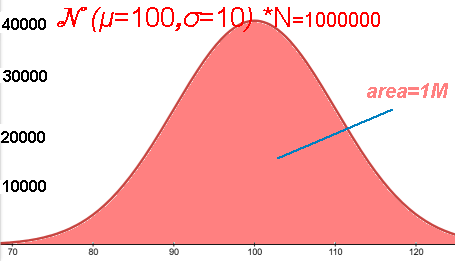
μ=100, blue σ=10, red σ=5 

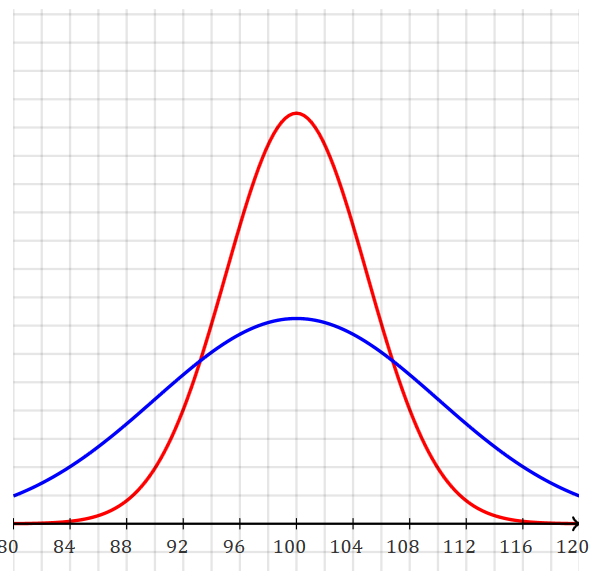
Mathpapa:
y=1/(10*sqrt(2*PI)) * e^(-(x-100)^2/(2*10^2))  ; y=1/(5*sqrt(2*PI)) * e^(-(x-100)^2/(2*5^2))  
Xmin: 80  Xmax:120   Ymin:-.01   Ymax: .1 

Desmos:
y=1/(10\sqrt{2\pi})\cdot e^{\frac{-\left(x-100\right)^{2}}{2\cdot10^{2}}}
X-axis: 80 to 120     Y-axis: 0 to .05

Any normal: Mathpapa
y=1/(s*sqrt(2*PI)) * e^(-(x-m)^2/(2*s^2))  @s=  ;m=
Desmos:
y=1/(s\cdot\sqrt{2\cdot\pi})\cdot e^{-\frac{\left(x-m\right)^{2}}{2s^{2}}}
Multiply by n or N.
u=10, blue s=1, red s=2, green s=3 
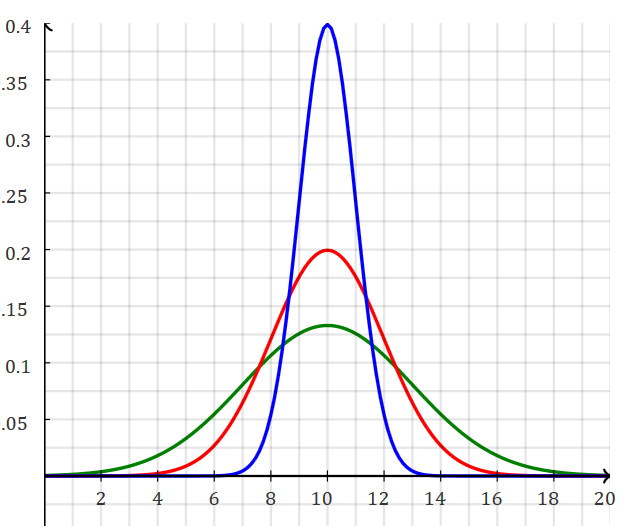
Mathpapa:
y=1/(1*sqrt(2*PI)) * e^(-(x-10)^2/(2*1^2))  ; y=1/(2*sqrt(2*PI)) * e^(-(x-10)^2/(2*2^2))  ; y=1/(3*sqrt(2*PI)) * e^(-(x-10)^2/(2*3^2))  
Xmin: 0  Xmax:20   Ymin:-.1   Ymax: .4

1-D standard normal distribution.

2-D normal distribution.
    

Genes example

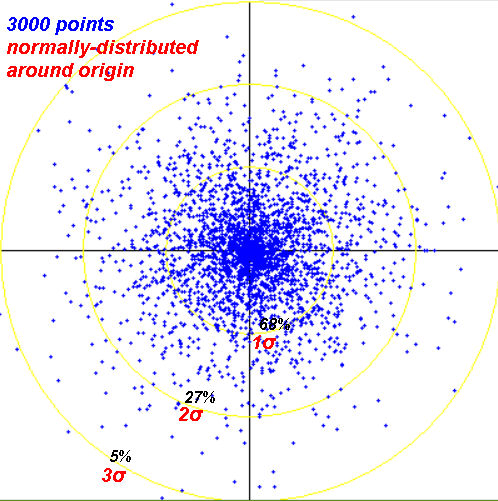
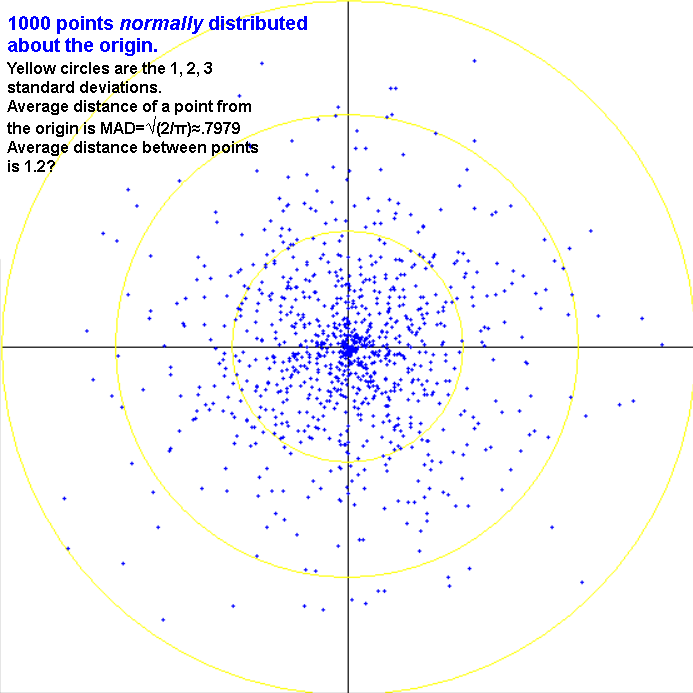
Average (or expected) difference between two data values randomly chosen from a normal distribution is 2σ/sqrt(pi) = 1.128σ = MAD√2

Two normal distributions (two independent normal RVs, W and Y).
Probability that a random from W is greater than a random from Y: RV D = W-Y is normal with
μd = μw - μy
σd = √[σ2w + σ2y]
P(W-Y>0) = P(D>0) → x = 0
Into above calculator to determine z and 1-CDF(z).

z (#std devs) y
0=μ 0.39894228
1 0.24197072
2 0.05399096
3 0.00443184
4 0.00013383
5 0.00000148

Number of times more frequent/common a row std dev is than a col std dev
1σ 2σ 3σ 4σ 5σ
0=μ 1.6 7.4 90 2981 268,337
1σ 4.5 55 1808 162,755
2σ 12 403 36,315
3σ 33 2981
4σ 90
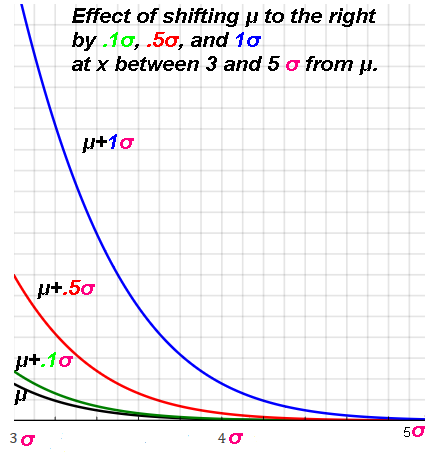
Relative number more at SD's when mean shifts to right
at SD= 1 2 3 4 5 6
μ=0 (baseline) 1 1 1 1 1 1
μ=0.1 1.100 1.215 1.343 1.484 1.640 1.813
μ=0.5 1.455 2.399 3.955 6.521 10.751 17.725
μ=1.0 1.649 4.482 12.182 33.115 90.017 244.692

Ex. When the mean shifts .5 SD to the right, there will be 3.955 times as much/many data at the original +3σ value as there was originally when μ was 0.

          √(2π)≈2.507     √π≈1.772

Alternate definitions of what's standard.

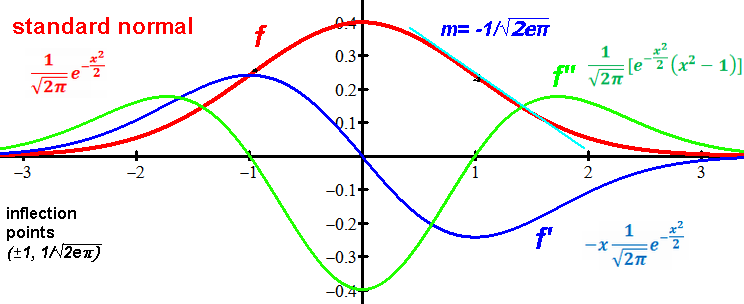
Derivatives of standard normal function: