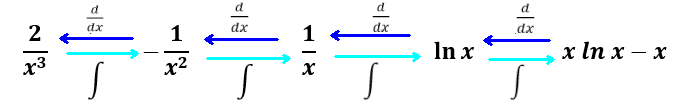Uses of derivatives: rate of change at any point of the function; where function ƒ is increasing, decreasing, and constant; find extrema (minimum and maximum values) of ƒ; find concavity ("bend") and inflection points (changes of concavity) of ƒ; use the tangent line to linearly approximate the function near a point.
Integral calculus:
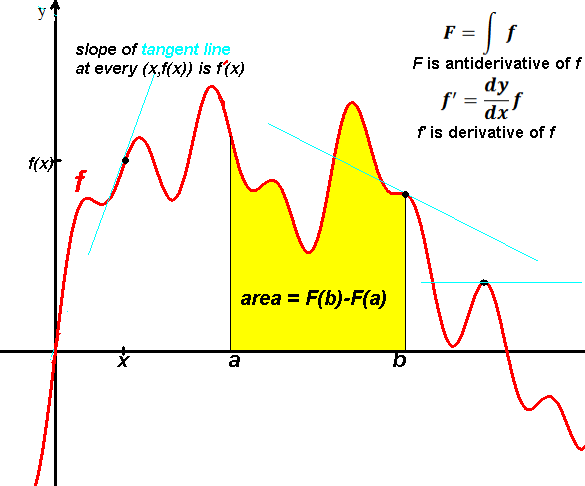
The antiderivative of a function ƒ is the function F(x)
whose derivative F'(x) is ƒ.
The integral of a function ƒ on an interval [a,b]
is the difference between the antiderivative values evaluated at the endpoints of the interval:
∫ƒ = F(b)-F(a).
Uses of integration: area under the curve of ƒ in the interval;
average function value;
length of a curve;
surface area and volume of surfaces of revolution.
Differential calculus, differentiation, and derivatives
Would like to know at each point on the curve of function ƒ what is the
rate of change, i.e. by how much the function is increasing or decreasing at
that point instantaneously, i.e. how fast or slow is ƒ changing.
This is defined as the slope of the line tangent to (i.e. just touching at)
the curve at that point.
On a curve, unlike on a line, the tangent line is different at each point
and thus the slope is too.
Between the endpoints of an interval around a point
the average rate of change can be calculated:
a secant line connects the endpoints; its slope Δy/Δx is the rate of change
between the endpoints, ie. the average rate of change;
Shrinking the interval's width to[ward] zero makes the secant line become the tangent line
to/at the point. As Δx→0 it becomes dx, the differential of x, ("d for darn small");
Δy becomes dy and dy/dx is the slope of the tangent line.
The dx is infinitesimally small ("a ghost of a departed quantity");
or it means that the denominator approaches 0.
The
tangent line
(that touches the curve at that point) is the
rate of change of the function at that point.
Its slope is the change of y per change of x, i.e. the rate of change.
This is the instantaneous rate of change, i.e. the rate of change at that single point.
The derivative of a function ƒ is the function ƒ' whose values
are the slope of the tangent line at each point on the curve of ƒ.
I.e. from your ƒ function you derive another function ƒ' which tells you the
slopes of the tangent lines at every point on the curve of ƒ.
Various techniques exist to find the derivative of most functions. Software can do it, too.
Given an x, ƒ(x) is the y value of a point on the curve of ƒ.
ƒ'(x) is the slope m of the line tangent to that (x,y) point on the curve of ƒ.
The derivative ƒ' tells you the slope of the tangent
line at a point on the curve of ƒ.
The tangent line is the best approximation of the curve.
This slope is the best constant approximation for a rate of change around the point.
This slope is what is meant by the instantaneous rate of change.
Differentiation (d/dx) is the process of determing what the derivative function is,
i.e. taking the derivative.
A function must be "nice" to have a derivative (at a point):
it must be continuous (i.e. no holes, jumps, vertical asymptotes)
and differentiable (i.e. smooth: point is not a kink/cusp/corner
(there being no 2-sided limit at such a point)
e.g. f(x)=|x| at x=0
nor a vertical tangent line (which has infinite slope)
e.g. f(x)=∛x at x=0 and f(x)=∛x2 at x=0).
Differentiability implies continuity.
Definition of the derivative of a function f is (using h instead of Δx):
lim h→0 [f(x+h)-f(x) / h]
Alternate notations for derivative function: ƒ'(x) dy/dx y' ̇y D[y]
Various rules and formulas exist for finding the derivative of categories of function,
e.g. polynomial, trigonometric, exponential etc. So to bypass using the definition
to determine the derivative.
(cf)' = cf'
Power rule: (xr)' = rxr-1
(f±g)' = f'±g'
Product rule: (fg)'= f'g + fg' (fgh)'= f'gh + fg'h + fgh' ...
Quotient rule: (f/g)' = (f'g-fg')/g2 (1/f)'=-f'/f2
Chain rule of a composition of functions: f(g(x))' = f'(g(x))g'
sin' = cos cos'=-sin tan'=sec2
(ex)' = ex (bx)' = (ln b)bx
(ln x)' = 1/x (logbx)' = 1/ x(ln b)
From algebra, know that x-intercepts of function ƒ are the solutions to
ƒ(x)=0. y-intercept = ƒ(0).
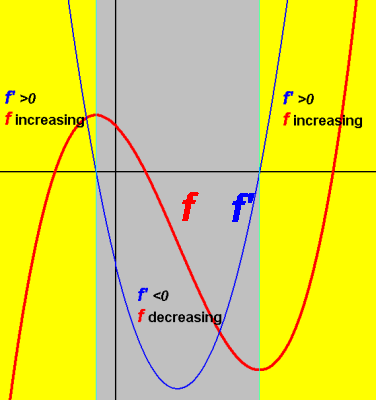
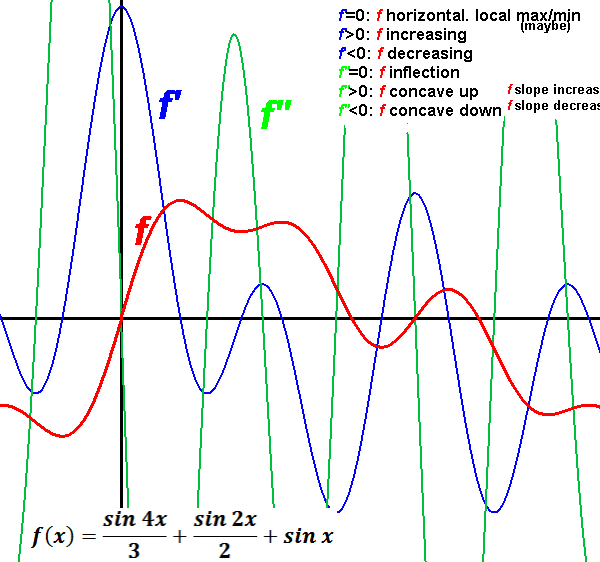
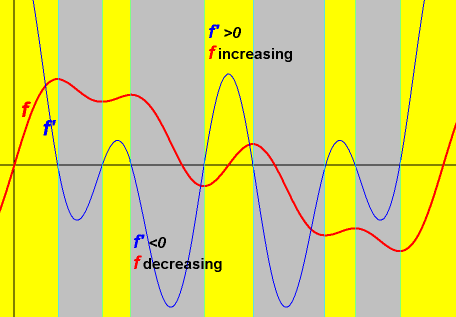
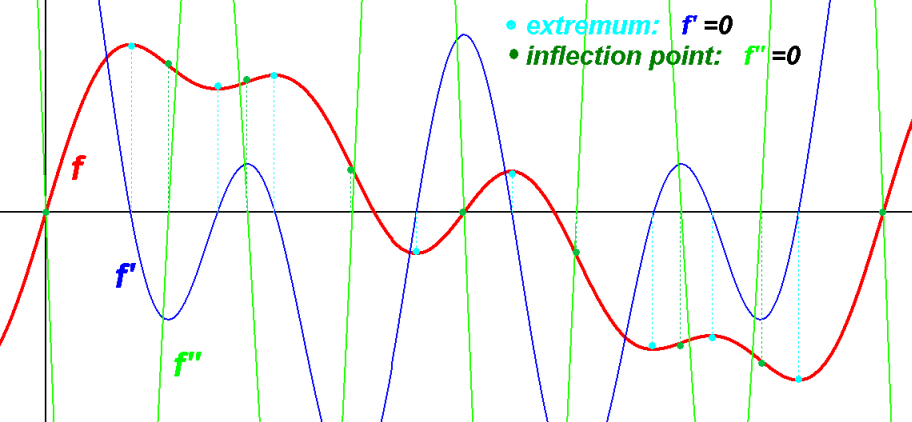
Derivative indicates where ƒ is increasing, decreasing, or horizontal:
ƒ'(x)>0 ie. derivative (i.e. slope of the tangent line) is positive, means ƒ is increasing at (x,ƒ(x)).
ƒ'(x)<0 ie. derivative is negative, means ƒ is decreasing at (x,ƒ(x)).
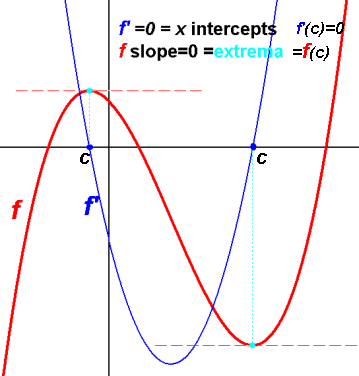
ƒ'(x)=0 ie. derivative is zero (ƒ' x-intercept), means ƒ is horizontal at (x,ƒ(x)).
Solve ƒ'(x)=0 to find x-intercepts of ƒ'.
X's where the derivative is zero (or doesn't exist, i.e. a cusp) are critical numbers c
which might be extrema, i.e. (local) maximum or minimum values of the function.
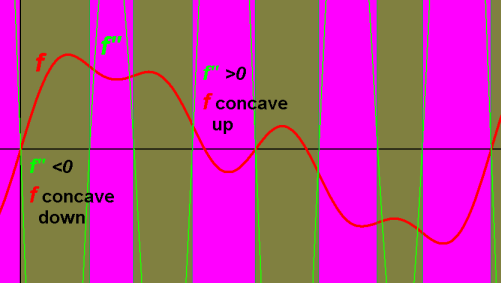
The second derivative ƒ''(x), the derivative of the derivative.
indicates the concavity/"bend" of the function ƒ:
ƒ''(x)>0 ie. 2nd derivative is positive, means ƒ is concave up, tangent line is below ƒ,
ƒ' slopes are increasing.
ƒ''(x)<0 ie. 2nd derivative is negative, means ƒ is concave down, tangent line is above ƒ,
ƒ' slopes are decreasing.
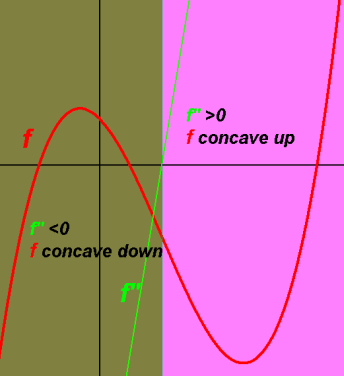
ƒ''(x)=0 ie. 2nd derivative is zero (ƒ'' x-intercept), [might be] inflection point
where concavity changes and
where the slope (rate of change) of ƒ is at a maximum or minimum.
Solve ƒ''(x)=0 to find x-intercepts of ƒ''.
At a critical number c, if ƒ''(c)>0 the extremum is a minimum.
At a critical number c, if ƒ''(c)<0 the extremum is a maximum.
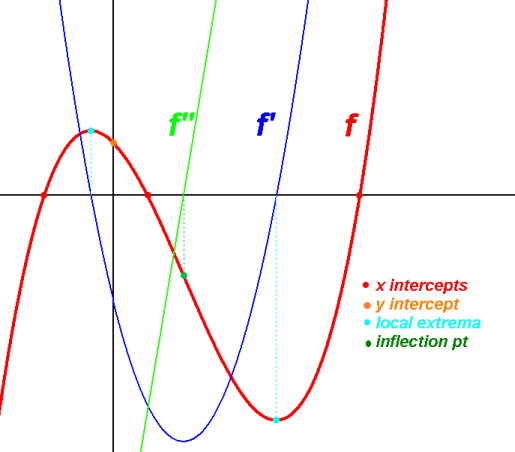
Another f function example:
The formula for the line tangent to the curve at the point (c,ƒ(c)) is y = ƒ'(c)x + ƒ(c)-ƒ'(c)c
Summary of derivatives' information of basic functions
Integral calculus, integration, and integrals
Would also like to know the area under the curve of the function ƒ over any interval [a,b].
Integration ∫ of the function to obtain its integral F.
F(b)-F(a) = area under the curve of function ƒ in the interval [a,b].
This area could represent something physical depending on the application,
such as time, energy, money, distance etc.
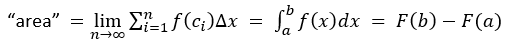F is the antiderivative of ƒ
Hundreds of rules and techniques exist to find integrals.
∫xndx= xn+1 / n+1, n≠-1
∫1/x dx= ln x
∫ex dx= ex
∫bx dx= bx / ln b
∫ln x dx= x(ln x - 1)
∫logbx dx= x(ln x - 1) / ln b
∫sin x dx= -cos x
∫cos x dx= sin x
∫cos(x2)dx= no closed form?
Area between two curves f(x) and g(x) is ∫(f(x)-g(x))dx
Volume of a solid of revolution:
disk method: V= ∫πf(x)2 dx
shell method: V= ∫2πx f(x) dx
Surface area of a solid of revolution:
around y: S= ∫2πx √(1+f'(x)2) dx
around x: S= ∫2πf(x) √(1+f'(x)2) dx
Arc length (length of curve): s= ∫√(1+f'(x)2) dx
Fundamental theorem of calulus: differentiation and integration are related:
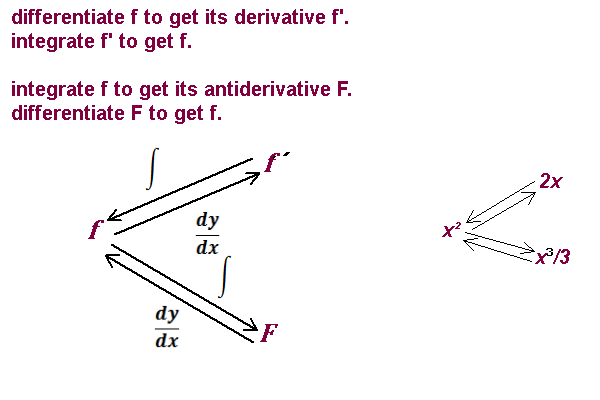
Integration can recover ƒ up to a constant; ƒ can slide up or down.
Example (in opposite directions):
