Ellipse:

set of points whose sum of distances d1+d2 to two foci F1,F2 are the same.
x and y both squared, and with different coefficients, either both positive or both negative: Ax2+Cy2+[Dx]+[Ey]-F=0, A≠C

Ellipses centered at origin (0,0):
  

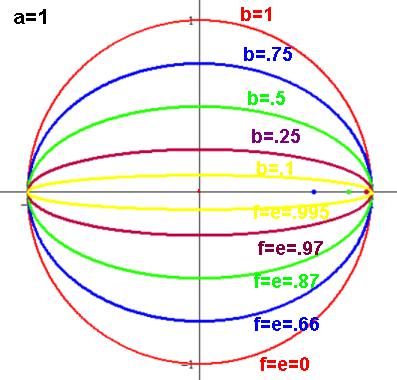
Eccentricity e is a measure of the ovalness/roundness of the ellipse. 0<e<1. Closer to 1: flatter, more eccentric. e=f/a
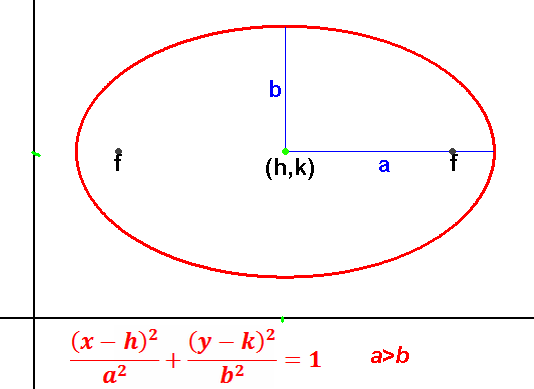
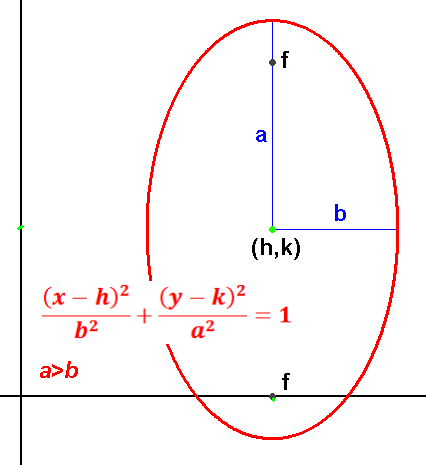
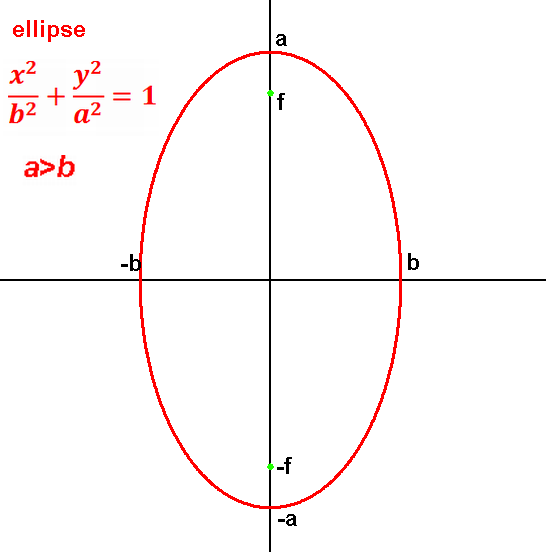
Ellipse is a deformed circle where one direction has been stretched more than the other direction.

Ellipses centered at (h,k):
  

Ellipses rotated:

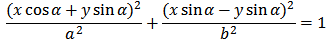
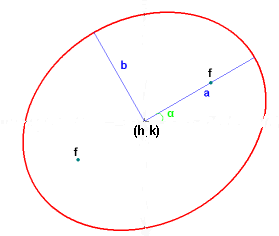
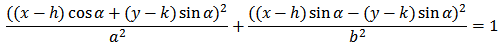
Given two foci F1 and F2, each different distance d gives a different ellipse with different a and b, and different eccentricity e:

Given a distance d, each different foci pair give a different ellipse with different b, and different eccentricity e:

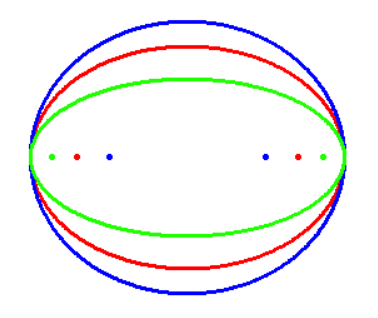
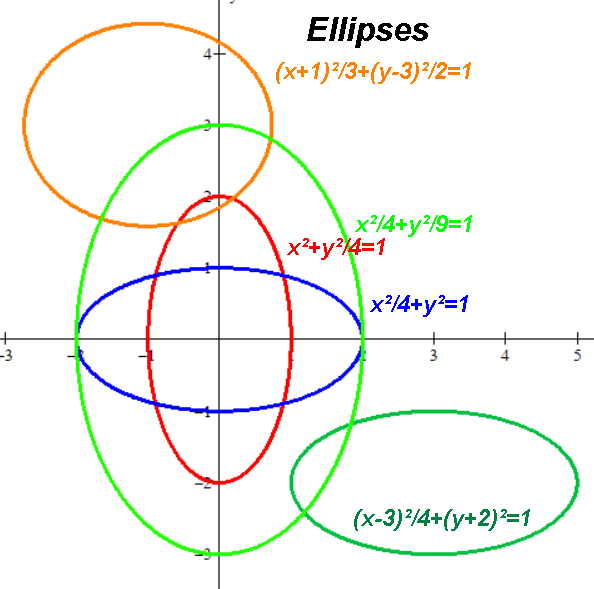
"Unit ellipses":

Area of an ellipse = πab.
There is no algebraic formula for the circumference. But various approximations to within .0015% accuracy exist. Simple: C≈2π((a+b)/2)
Ramanujan: C≈π[3(a+b)-√((3a+b)(a+3b))]
Circle is an ellipse in which a=b, the eccentricity e is 0, and the two foci are the same point, the center of the circle.
Java applet to draw ellipse.

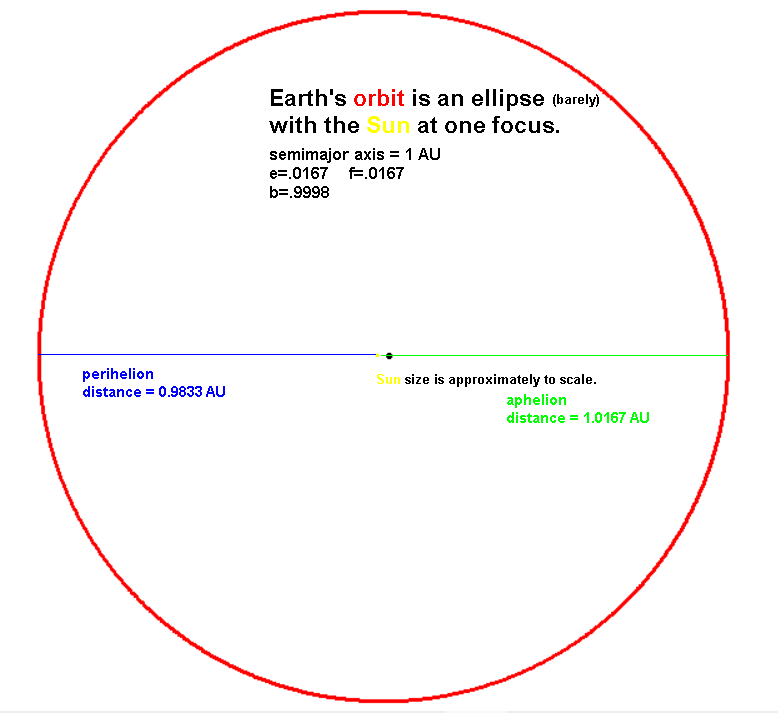
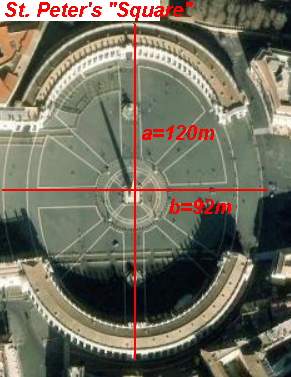
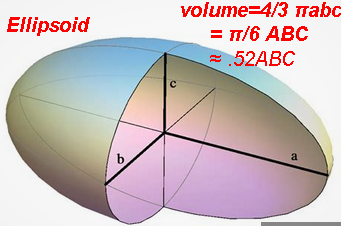
Ellipsoid
2 axes same: spheroid
3 axes different: tri-axial ellipsoid